题目内容
4．对于正项数列{an}，定义Hn=$\frac{n}{{a}_{1}+2{a}_{2}+3{a}_{3}+…+n{a}_{n}}$为{an}的“光阴”值，现知某数列的“光阴”值为Hn=$\frac{2}{n+3}$，则数列{an}的通项公式为（ ）| A． | an=$\frac{n+1}{n}$ | B． | an=$\frac{2n+1}{n}$ | C． | an=$\frac{2n+1}{2n}$ | D． | an=$\frac{3n+1}{2n}$ |
分析 通过定义及Hn=$\frac{2}{n+3}$可得a1+2a2+…+nan=$\frac{n（n+3）}{2}$、a1+2a2+…+（n-1）an-1=$\frac{（n-1）（n+2）}{2}$，两式相减，进而计算可得结论．
解答 解：∵Hn=$\frac{n}{{a}_{1}+2{a}_{2}+3{a}_{3}+…+n{a}_{n}}$，
∴a1+2a2+…+nan=$\frac{n}{{H}_{n}}$，
又∵Hn=$\frac{2}{n+3}$，
∴a1+2a2+…+nan=$\frac{n（n+3）}{2}$，
a1+2a2+…+（n-1）an-1=$\frac{（n-1）（n+2）}{2}$，
两式相减得：nan=$\frac{n（n+3）}{2}$-$\frac{（n-1）（n+2）}{2}$=$\frac{2n+2}{2}$，
∴an=$\frac{n+1}{n}$，
故选：A．
点评 本题考查新定义，考查数列的通项，解题的关键是理解新定义，注意解题方法的积累，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
15．沙坪坝凯瑞商都于2015年4月24日重新装修开业，某调查机构通过调查问卷的形式对900名顾客进行购物满意度调查，并随机抽取了其中30名顾客（女16名．男14名）的得分（满分50分），如表1：
表1
（Ⅰ）根据以上数据，估计这900名顾客中得分大于45分的人数；
（Ⅱ）现用计算器求得这30名顾客的平均得分为40.5分，若规定大于平均分为“满意”，
否则为“不满意”，请完成表2：
表2
（Ⅲ）根据上述表中数据，利用独立性检验的方法判断，能否在犯错误的概率不超过1%的前提下，认为顾客“性别”与“购物是否满意”有关？
参考公式和数据：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
表1
| 女 | 47 | 36 | 32 | 48 | 34 | 44 | 43 | 47 | 46 | 41 | 43 | 42 | 50 | 43 | 35 | 49 |
| 男 | 37 | 35 | 34 | 43 | 46 | 36 | 38 | 40 | 39 | 32 | 48 | 33 | 40 | 34 |
（Ⅱ）现用计算器求得这30名顾客的平均得分为40.5分，若规定大于平均分为“满意”，
否则为“不满意”，请完成表2：
表2
| “满意”的人数 | “不满意”的人数 | 合计 | |
| 女 | 16 | ||
| 男 | 14 | ||
| 合计 | 40 |
参考公式和数据：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
| P（k2≥k） | 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
19．
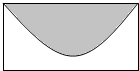如图的矩形，长为5，宽为2，在矩形内随机地撒300颗黄豆，数得落在阴影部分的黄豆数为138颗，则可以估计出阴影部分的面积约为（ ）
如图的矩形，长为5，宽为2，在矩形内随机地撒300颗黄豆，数得落在阴影部分的黄豆数为138颗，则可以估计出阴影部分的面积约为（ ）| A． | $\frac{23}{11}$ | B． | $\frac{23}{10}$ | C． | $\frac{23}{6}$ | D． | $\frac{23}{5}$ |
在平面直角坐标系中，圆O：x2+y2=4与x轴的正半轴交于点A，以A为圆心的圆A：（x-2）2+y2=r2（r＞0）与圆O交于B，C两点．
17．为了得到函数$y=sin（x-\frac{π}{3}）（x∈R）$的图象，只需把函数y=sinx的图象上所有的点（ ）
| A． | 向右平移$\frac{π}{3}$个单位长度 | B． | 向右平移$\frac{π}{6}$个单位长度 | ||
| C． | 向左平移$\frac{π}{3}$个单位长度 | D． | 向左平移$\frac{π}{6}$个单位长度 |