题目内容
9.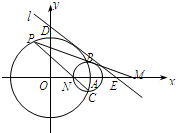 在平面直角坐标系中,圆O:x2+y2=4与x轴的正半轴交于点A,以A为圆心的圆A:(x-2)2+y2=r2(r>0)与圆O交于B,C两点.
在平面直角坐标系中,圆O:x2+y2=4与x轴的正半轴交于点A,以A为圆心的圆A:(x-2)2+y2=r2(r>0)与圆O交于B,C两点.(1)若直线l与圆O切于第一象限,且与坐标轴交于D,E,当线段DE长最小时,求直线l的方程;
(2)设P是圆O上异于B,C的任意一点,直线PB、PC分别与x轴交于点M和N,问OM•ON是否为定值?若是,请求出该定值;若不是,请说明理由.
分析 (1)由截距式设直线l的方程为$\frac{x}{a}$+$\frac{y}{b}$=1(a>0,b>0),从而可得$\frac{{|{ab}|}}{{\sqrt{{a^2}+{b^2}}}}=2$,再由基本不等式可得$D{E^2}={a^2}+{b^2}=4(\frac{1}{a^2}+\frac{1}{b^2})({a^2}+{b^2})≥16$,从而解得.
(2)设B(x0,y0),P(x1,y1)(y1≠±y0),则C(x0,-y0),$x_0^2+y_0^2=4$,$x_1^2+y_1^2=4$,写出直线PB与直线PC的方程,从而得到M,N的坐标,从而求OM•ON即可.
解答 解:(1)设直线l的方程为$\frac{x}{a}$+$\frac{y}{b}$=1(a>0,b>0),
即bx+ay-ab=0,
由直线l与圆O相切得$\frac{{|{ab}|}}{{\sqrt{{a^2}+{b^2}}}}=2$,
即$\frac{1}{a^2}+\frac{1}{b^2}=\frac{1}{4}$,
$D{E^2}={a^2}+{b^2}=4(\frac{1}{a^2}+\frac{1}{b^2})({a^2}+{b^2})≥16$,
(当且仅当$a=b=2\sqrt{2}$时取等号),
此时直线l的方程为$x+y-2\sqrt{2}=0$.
(2)设B(x0,y0),P(x1,y1)(y1≠±y0),
则C(x0,-y0),$x_0^2+y_0^2=4$,$x_1^2+y_1^2=4$,
直线PB的方程为:$y-{y_1}=\frac{{{y_0}-{y_1}}}{{{x_0}-{x_1}}}(x-{x_1})$,
直线PC的方程为:$y-{y_1}=\frac{{-{y_0}-{y_1}}}{{{x_0}-{x_1}}}(x-{x_1})$,
分别令y=0,得${x_M}=\frac{{{x_1}{y_0}-{x_0}{y_1}}}{{{y_0}-{y_1}}},{x_N}=\frac{{{x_1}{y_0}+{x_0}{y_1}}}{{{y_0}+{y_1}}}$,
所以OM•ON=$|{{x_M}{x_N}}|=|{\frac{x_1^2y_0^2-x_0^2y_1^2}{y_0^2-y_1^2}}|=|{\frac{(4-y_1^2)y_0^2-(4-y_0^2)y_1^2}{y_0^2-y_1^2}}|=4$为定值.
点评 本题考查了直线与圆的位置关系的应用及化简运算的能力,属于中档题.

| A. | $\frac{{x}^{2}}{45}$+$\frac{{y}^{2}}{{18}^{2}}$=1 | B. | $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{27}$=1 | C. | $\frac{{x}^{2}}{27}$+$\frac{{y}^{2}}{18}$=1 | D. | $\frac{{x}^{2}}{18}$+$\frac{{y}^{2}}{9}$=1 |
| A. | an=$\frac{n+1}{n}$ | B. | an=$\frac{2n+1}{n}$ | C. | an=$\frac{2n+1}{2n}$ | D. | an=$\frac{3n+1}{2n}$ |
| A. | $\frac{1}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{5}{32}$ | D. | $-\frac{27}{32}$ |
 对于下列命题:
对于下列命题: