题目内容
19．
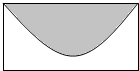如图的矩形，长为5，宽为2，在矩形内随机地撒300颗黄豆，数得落在阴影部分的黄豆数为138颗，则可以估计出阴影部分的面积约为（ ）| A． | $\frac{23}{11}$ | B． | $\frac{23}{10}$ | C． | $\frac{23}{6}$ | D． | $\frac{23}{5}$ |
分析 根据几何概型的公式，求出阴影部分的面积即可．
解答 解：根据题意得，该题目是几何概型的应用问题，
设阴影部分的面积为S，则
$\frac{S}{5×2}$=$\frac{138}{300}$，
解得S=$\frac{23}{5}$．
故选：D．
点评 本题考查了几何概型的应用问题，是基础题目．
练习册系列答案
相关题目
10．若a，b∈R，则不等式|2+ax|≥|2x+b|的解集为R的充要条件是（ ）
| A． | a=±2 | B． | a=b=±2 | C． | ab=4且|a|≤2 | D． | ab=4且|a|≥2 |
14．设f（x）=${∫}_{-x}^{x}$cos2tdt，则f（f（$\frac{π}{4}$））=
| A． | 1 | B． | sin 1 | C． | sin 2 | D． | 2sin 4 |
4．对于正项数列{an}，定义Hn=$\frac{n}{{a}_{1}+2{a}_{2}+3{a}_{3}+…+n{a}_{n}}$为{an}的“光阴”值，现知某数列的“光阴”值为Hn=$\frac{2}{n+3}$，则数列{an}的通项公式为（ ）
| A． | an=$\frac{n+1}{n}$ | B． | an=$\frac{2n+1}{n}$ | C． | an=$\frac{2n+1}{2n}$ | D． | an=$\frac{3n+1}{2n}$ |
11．函数f（x）=x+2cosx在区间[0，π]上的最大值为（ ）
| A． | 2 | B． | π-2 | C． | $\sqrt{3}+\frac{5π}{6}$ | D． | $\sqrt{3}+\frac{π}{6}$ |