题目内容
2．
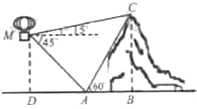如图，在离地面高400m的热气球上，观测到山顶C处的仰角为15°，山脚A处的俯角为45°，已知∠BAC=60°，则山的高度BC为（ ）| A． | 700 m | B． | 640 m | C． | 600 m | D． | 560 m |
分析 首先在Rt△AMD中，算出AM的值，然后在△MAC中，利用正弦定理算出AC的值，最后在Rt△ABC中，利用三角函数的定义即可算出山的高度BC．
解答 解：根据题意，可得Rt△AMD中，∠MAD=45°，MD=14200，
∴AM=$\frac{MD}{sin45°}$=400$\sqrt{2}$．
∵△MAC中，∠AMC=45°+15°=60°，
∠MAC=180°-45°-60°=75°，
∴∠MCA=180°-∠AMC-∠MAC=60°，
由正弦定理，得$AC=\frac{MAsin∠AMC}{sin∠MCA}$=$\frac{400\sqrt{2}×\frac{\sqrt{3}}{2}}{\frac{\sqrt{2}}{2}}$=400$\sqrt{3}$，
在Rt△ABC中，BC=ACsin∠BAC=400$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=600m．
故选：C
点评 本题主要考查解三角形的实际应用问题．着重考查了三角函数的定义、利用正弦定理解三角形等知识，属于中档题．
练习册系列答案
相关题目
10．设$a={log_2}π，b={log_{\frac{1}{2}}}π，c=\frac{1}{π^2}$则（ ）
| A． | a＞b＞c | B． | b＞a＞c | C． | a＞c＞b | D． | c＞b＞a |
17．设f0（x）=cosx，f1（x）=f0′（x），f2（x）=f1′（x），…，fn+1（x）=fn′（x）（n∈N），则f2015（x）=（ ）
| A． | sinx | B． | -sinx | C． | cosx | D． | -cosx |
14．在如图所示的平面图形中，$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$为互相垂直的单位向量，则向量$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$可表示为（ ）
| A． | $\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$ | B． | -$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$ | C． | -$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$ | D． | 3$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$ |