题目内容

14．对如图，定义在[-1，+∞）上的函数f（x）的图象由一条线段及抛物线的一部分组成，求f（x）的解析式．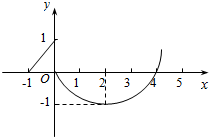

分析 分别设出函数的解析式，由待定系数法可得．

解答 解：当-1≤x≤0时，设解析式为y=kx+b，
由图象有$\left\{\begin{array}{l}{-k+b=0}\\{b=1}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$，∴y=x+1．
当x＞0时，设解析式为y=a（x-2）2-1，
∵图象过点（4，0），
∴0=a（4-2）2-1，解得a=$\frac{1}{4}$．
∴y=$\frac{1}{4}$（x-2）2-1．
综上，函数f（x）在[-1，+∞）上的解析式为f（x）=$\left\{\begin{array}{l}{x+1，-1≤x≤0}\\{\frac{1}{4}（x-2）^{2}-1，x＞0}\end{array}\right.$

点评 本题考查分段函数的解析式，涉及一次函数和二次函数解析式，属基础题．

练习册系列答案
相关题目
4．已知函数f（x）=a-be-x的图象在x=0处的切线方程为y=x．（e是自然对数的底数，e=2.71828…）
（Ⅰ） 求a，b的值；
（Ⅱ） 若g（x）=mlnx-e-x+$\frac{1}{2}$x2-（m+1）x+1（m＞0），求函数h（x）=g（x）-f（x）的单调区间．
5．椭圆$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），两焦点F1，F2，P为椭圆上一点，若存在$\overrightarrow{P{F}_{1}}$$•\overrightarrow{P{F}_{2}}$=c2，求e的范围．
2．在△ABC中，D、E分别为边BC、AC的中点．F为边AB上的点，且$\overrightarrow{AB}$=3$\overrightarrow{AF}$，若$\overrightarrow{AD}$=x$\overrightarrow{AF}$+y$\overrightarrow{AE}$，x，y∈R，则x=$\frac{3}{2}$，y=1．
9．已知数列{an}满足a1=1，an=logn（n+1）（n≥2，n∈N*），定义：使乘积a1•a2•…•ak为正整数的k（k∈N*）叫做“简易数”．则在[3，2013]内所有“简易数”的和为2035．
19．若函数$f（x）=\frac{a}{x^2}$在（2，f（2））处的切线过点（1，2），则a=（　　）
A．4B．7C．8D．$\frac{8}{5}$
6．已知正项等比数列{an}的前n项和为Sn，若-3，S5，S10成等差数列，则S15-S10的最小值为（　　）
A．8B．9C．10D．12
3．已知函数f（x）=3ax-4bx且a=log32，又函数y=logc（x+1）+1（c＞0且c≠1）图象恒过定点的纵坐标为b．
（1）求函数f（x）的解析式；
（2）求函数y=f（x）在[-1，1]内的值域．
4．设函数f（x）=$\left\{\begin{array}{l}{{2}^{x}，}&{x≥0}\\{-x，}&{x＜0}\end{array}\right.$．
（1）f（x）有零点吗？
（2）设g（x）=f（x）+k，为了使方程g（x）=0有且只有一个根，k应该怎样限制？
（3）当k=-1时，g（x）有零点吗？若果有，把它求出来，如果没有，请说明理由；
（4）你给k规定一个范围，使得方程g（x）=0总有两个根．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网