题目内容

14．函数f（x）=$\frac{{x}^{2}-x}{{e}^{x}}$的大致图象是（　　）
A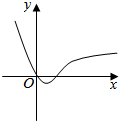．B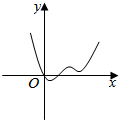．C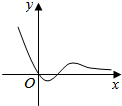．D．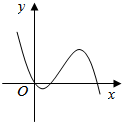

分析 根据函数的解析式，利用导数法分析函数的单调性，并求出函数的零点，排除不满足条件的答案，可得结论．

解答 解：∵函数f（x）=$\frac{{x}^{2}-x}{{e}^{x}}$，
∴f′（x）=$\frac{{3x-x}^{2}}{{e}^{x}}$，
令f′（x）=0，则x=0或3，
当x＜0，或x＞3时，f′（x）＜0，此时函数为减函数，
当0＜x＜3时，f′（x）＞0，此时函数为增函数，
故排除A，B，
令f（x）=0，则x=0或1，
故函数只有两个零点，
故排除D，
故选：C

点评 本题考查的知识点是函数的图象，分析出函数的单调性及零点个数，是解答的关键．

练习册系列答案
相关题目
4．y=|sinx|的一个单调增区间为（　　）
A．（-$\frac{π}{4}$，$\frac{π}{4}$）B．（$\frac{π}{4}$，$\frac{3π}{4}$）C．（π，$\frac{5π}{4}$）D．（$\frac{3π}{2}$，2π）
5．已知函数f（x）=ax2+2ax+1在区间[-1，2]上有最大值4，求实数a的值．
2．解关于x的不等式$\frac{{x}^{2}-x+3}{{x}^{2}+ax}$＞0（a≠0）
9．（1）随机变量ξ的分布列如下：
 ξ-1 0 1 
 Pa b  c
其中a、b、c成等差数列，则P（|ξ|=1）=$\frac{2}{3}$，公差d的取值范围是[-$\frac{1}{3}$，$\frac{1}{3}$]．
（2）设离散型随机变量X的分布列为
 X0 1 2 3 4 
 P0.2 0.1 0.1 0.3  m
求：①2X+1的分布列；②|X-1|的分布列．
19．已知函数f（x）=x3-$\frac{3}{2}$ax2+1（x∈R，a＞1）在区间x∈[-1，1]上最小值为-2．
（1）求a的值以及f（x）在x∈R时的极值；
（2）若函数g（x）=f（x）-mx在区间x∈[-2，2]上为减函数，求实数m的取值范围．
6．已知直线y=a与函数f（x）=|x2-4x|的图象恰有3个交点，则a=4．
3．求下列不等式的解集
（1）|x+1|-|2x-6|＞3
（2）x+$\frac{2}{x+1}$＞2．
4．已知函数f（x）=$\frac{{x}^{2}}{1+{x}^{2}}$
（1）求f（2）+f（$\frac{1}{2}$），f（3）+f（$\frac{1}{3}$）的值；
（2）求证：f（x）+f（$\frac{1}{x}$）是定值；
（3）求f（2）+f（$\frac{1}{2}$）+f（3）+f（$\frac{1}{3}$）+…+f（2012）+f（$\frac{1}{2012}$）的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网