题目内容
19.已知函数f(x)=x3-$\frac{3}{2}$ax2+1(x∈R,a>1)在区间x∈[-1,1]上最小值为-2.(1)求a的值以及f(x)在x∈R时的极值;
(2)若函数g(x)=f(x)-mx在区间x∈[-2,2]上为减函数,求实数m的取值范围.
分析 (1)求导,利用闭区间最值的判断求a的值.利用导数求极值
(2)在区间x∈[-2,2]上为减函数,知g′(x)≤0在x∈[-2,2]上恒成立.
解答 (1)f′(x)=3x2-3ax,
令f′(x)=0,得x1=0,x2=a,
∵a>1,
在[-1,0]上,f′(x)>0;在[0,1]上,f′(x)<0
∴f(x)在[-1,0]上为增函数,在[0,1]上为减函数.
∵f(-1)=-$\frac{3}{2}$a,f(1)=2-$\frac{3}{2}$a,
∴f(-1)<f(1),
∴f(-1)=-2,a=$\frac{4}{3}$.
∵f(x)在(-∞,0)和(a,+∞)上为增函数,在[0,a]上为减函数
∴f(0)=1为极大值,f(a)=-$\frac{5}{27}$为极小值.
(2)g(x)=x3-2x2-mx+1,g′(x)=3x2-4x-m.
由g(x)在[-2,2]上为减函数,知g′(x)≤0在x∈[-2,2]上恒成立.
∴g′(-2)<0且g′(2)<0
即 m>20且m>4
∴m≥20.
∴实数m的取值范围是m≥20.
点评 考察了闭区间求最值,利用导数求极致,导函数的利用.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
11.2015年高中学业水平考试之后,为了调查同学们的考试成绩,随机抽查了某高中的高二一班的10名同学的语文、数学、英语成绩,已知其考试等级分为A,B,C,现在对他们的成绩进行量化:A级记为2分,B级记为1分,C级记为0分,用(x,y,z)表示每位同学的语文、数学、英语的得分情况,再用综合指标w=x+y+z的值评定该同学的得分等级.若w≥4,则得分等级为一级;若2≤w≤3.则得分等级为二级;若0≤w≤1,则得分等级为三级.得到如下结果:
(Ⅰ)在这10名同学中任取两人,求这两位同学英语得分相同的概率;
(Ⅱ)从得分等级是一级的同学中任取一人,其综合指标为a,从得分等级不是一级的同学中任取一人,其综合指标为b,记随机变量X=a-b,求X的分布列及其数学期望.
| 人员编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
| (x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (0,0,1) | (1,2,1) | (1,2,2) | (1,1,1) | (1,2,2) | (1,2,1) | (1,1,1) |
(Ⅱ)从得分等级是一级的同学中任取一人,其综合指标为a,从得分等级不是一级的同学中任取一人,其综合指标为b,记随机变量X=a-b,求X的分布列及其数学期望.
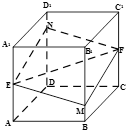 如图所示,正方体ABCD-A1B1C1D1的棱长为1,E、F分别是棱AA1、CC1的中点,过直线EF的平面分别与棱BB1,DD1交于M、N两点,设BM=x,x∈[0,1],给出以下四个命题:
如图所示,正方体ABCD-A1B1C1D1的棱长为1,E、F分别是棱AA1、CC1的中点,过直线EF的平面分别与棱BB1,DD1交于M、N两点,设BM=x,x∈[0,1],给出以下四个命题: