题目内容
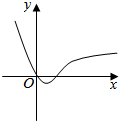
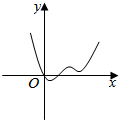
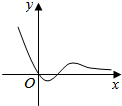
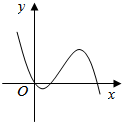
6．已知直线y=a与函数f（x）=|x2-4x|的图象恰有3个交点，则a=4．分析 若函数y=|x2-4x|与函数y=a有3个交点，可由函数图象的对折变换先画出函数y=|x2-4x|的图象，结合图象可得实数a的取值范围
解答 
解：函数y=|x2-4x|的图象如右图所示：
结合图象可得：
当a=4时函数y=|x2-4x|与y=a的图象有3个交点，
故答案为：4．
点评 本题考查了根的存在性及根的个数判断，以及函数与方程的思想，解答关键是运用数形结合的思想，属于中档题
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
1．数列1×$\frac{1}{2}$，2×$\frac{1}{4}$，3×$\frac{1}{8}$，4×$\frac{1}{16}$，…的前n项和为（ ）
| A． | 2-$\frac{1}{{2}^{n}}$-$\frac{n}{{2}^{n+1}}$ | B． | 2-$\frac{1}{{2}^{n-1}}$-$\frac{n}{{2}^{n}}$ | C． | $\frac{1}{2}$（n2+n+2）-$\frac{1}{{2}^{n}}$ | D． | $\frac{1}{2}$（n+1）n+1-$\frac{1}{{2}^{n+1}}$ |
11．2015年高中学业水平考试之后，为了调查同学们的考试成绩，随机抽查了某高中的高二一班的10名同学的语文、数学、英语成绩，已知其考试等级分为A，B，C，现在对他们的成绩进行量化：A级记为2分，B级记为1分，C级记为0分，用（x，y，z）表示每位同学的语文、数学、英语的得分情况，再用综合指标w=x+y+z的值评定该同学的得分等级．若w≥4，则得分等级为一级；若2≤w≤3．则得分等级为二级；若0≤w≤1，则得分等级为三级．得到如下结果：
（Ⅰ）在这10名同学中任取两人，求这两位同学英语得分相同的概率；
（Ⅱ）从得分等级是一级的同学中任取一人，其综合指标为a，从得分等级不是一级的同学中任取一人，其综合指标为b，记随机变量X=a-b，求X的分布列及其数学期望．
| 人员编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
| （x，y，z） | （1，1，2） | （2，1，1） | （2，2，2） | （0，0，1） | （1，2，1） | （1，2，2） | （1，1，1） | （1，2，2） | （1，2，1） | （1，1，1） |
（Ⅱ）从得分等级是一级的同学中任取一人，其综合指标为a，从得分等级不是一级的同学中任取一人，其综合指标为b，记随机变量X=a-b，求X的分布列及其数学期望．