题目内容
4.若函数y=f(x-1)的图象过点(2,3),则( )| A. | f(2)=3 | B. | f(3)=2 | C. | f(1)=3 | D. | f(3)=1 |
分析 由已知中函数y=f(x-1)的图象过点(2,3),可得f(2-1)=3,整理可得答案.
解答 解:∵函数y=f(x-1)的图象过点(2,3),
∴f(2-1)=3,
即f(1)=3,
故选:C.
点评 本题考查的知识点是函数的值,图象上的点与方程的关系,难度不大,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.设ω>0,函数f(x)=2tanωx的最小正周期为T,若f(x)是区间$(-\frac{π}{3},\frac{π}{4})$上的单调函数,则T的取值范围是[$\frac{2π}{3}$,+∞).
14.计算sin77°cos47°-sin13°cos43°的值等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
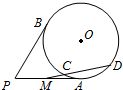 如图,P是圆O外一点,PA,PB是圆O的两条切线,切点分别为A,B,PA中点为M,过M作圆O的一条割线交圆O于C,D两点,若PB=8,MC=2,则CD=6.
如图,P是圆O外一点,PA,PB是圆O的两条切线,切点分别为A,B,PA中点为M,过M作圆O的一条割线交圆O于C,D两点,若PB=8,MC=2,则CD=6.