题目内容
(本题满分12分)探究函数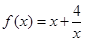 ,
, 的最小值,并确定取得最小值时
的最小值,并确定取得最小值时 的值,列表如下:
的值,列表如下:
请观察表中 值随
值随 值变化的特点,完成下列问题:
值变化的特点,完成下列问题:
(1) 当 时,
时,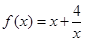 在区间
在区间 上递减,在区间 上递增;
上递减,在区间 上递增;
所以, = 时,
= 时,  取到最小值为 ;
取到最小值为 ;
(2) 由此可推断,当 时,
时,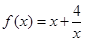 有最 值为 ,此时
有最 值为 ,此时 = ;
= ;
(3) 证明: 函数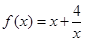 在区间
在区间 上递减;
上递减;
(4) 若方程 在
在 内有两个不相等的实数根,求实数
内有两个不相等的实数根,求实数 的取值范围。
的取值范围。
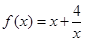 ,
, 的最小值,并确定取得最小值时
的最小值,并确定取得最小值时 的值,列表如下:
的值,列表如下: | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
 | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.102 | 4.24 | 4.3 | 5 | 5.8 | 7.57 | … |
 值随
值随 值变化的特点,完成下列问题:
值变化的特点,完成下列问题:(1) 当
 时,
时,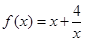 在区间
在区间 上递减,在区间 上递增;
上递减,在区间 上递增;所以,
 = 时,
= 时,  取到最小值为 ;
取到最小值为 ;(2) 由此可推断,当
 时,
时,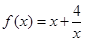 有最 值为 ,此时
有最 值为 ,此时 = ;
= ;(3) 证明: 函数
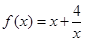 在区间
在区间 上递减;
上递减;(4) 若方程
 在
在 内有两个不相等的实数根,求实数
内有两个不相等的实数根,求实数 的取值范围。
的取值范围。(1)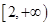 ;2 ,4 ; (2)最大值 -4;
;2 ,4 ; (2)最大值 -4;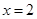 (3)略(4)
(3)略(4)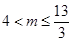
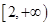 ;2 ,4 ; (2)最大值 -4;
;2 ,4 ; (2)最大值 -4;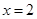 (3)略(4)
(3)略(4)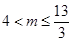
解:(1)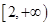 ;2 ,4 ;
;2 ,4 ;
(2)最大值 -4;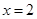
(1)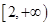 ;2 ,4 ;
;2 ,4 ;
(2)最大值 -4;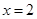 证明:设
证明:设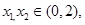 且
且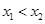 ,
,
则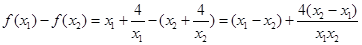
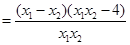 ;
;
∵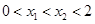 ,∴
,∴ ;
;
∴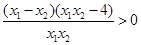 ,即
,即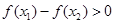 ;
;
∴函数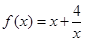
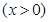 在区间
在区间 上递减。
上递减。
(4)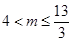
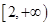 ;2 ,4 ;
;2 ,4 ; (2)最大值 -4;
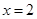
(1)
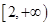 ;2 ,4 ;
;2 ,4 ; (2)最大值 -4;
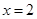 证明:设
证明:设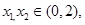 且
且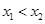 ,
, 则
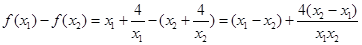
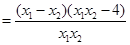 ;
; ∵
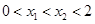 ,∴
,∴ ;
;∴
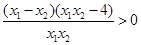 ,即
,即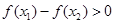 ;
; ∴函数
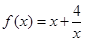
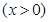 在区间
在区间 上递减。
上递减。(4)
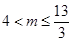

练习册系列答案
相关题目
 且
且 ,
,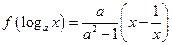
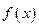 的表达式; (2)判断
的表达式; (2)判断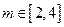 时,
时,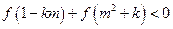 恒成立,求
恒成立,求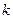 的取值范围.
的取值范围.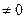 )恒有f(ab)=f(a)+f(b)且x>1时f(x)>0 ,f(2)=1
)恒有f(ab)=f(a)+f(b)且x>1时f(x)>0 ,f(2)=1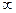 )上是增函数;
)上是增函数;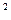 -5)<2.
-5)<2.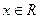 ,f(x+2)="--" f(x),当
,f(x+2)="--" f(x),当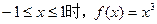 .
.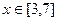 时,求f(x)的解析式。
时,求f(x)的解析式。 的定义域为 .
的定义域为 .
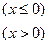 ,使函数值为5的
,使函数值为5的
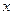 的值是( )
的值是( ) 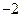
 或
或

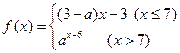
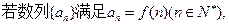 且
且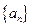 是递增数列,那么实数a的取值范围是 ( )
是递增数列,那么实数a的取值范围是 ( )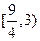


 .
.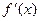 >0,
>0,  >0,则x<0时( )
>0,则x<0时( )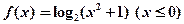 的反函数是_______ ___.
的反函数是_______ ___.