题目内容
(本小题10分)
对于函数f(x)(x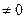 )恒有f(ab)=f(a)+f(b)且x>1时f(x)>0 ,f(2)=1
)恒有f(ab)=f(a)+f(b)且x>1时f(x)>0 ,f(2)=1
(1)求f(4)、f(1)、f(-1)的值;
(2)求证f(x)为偶函数;
(3)求证f(x)在(0,+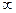 )上是增函数;
)上是增函数;
(4)解不等式f(x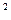 -5)<2.
-5)<2.
对于函数f(x)(x
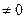 )恒有f(ab)=f(a)+f(b)且x>1时f(x)>0 ,f(2)=1
)恒有f(ab)=f(a)+f(b)且x>1时f(x)>0 ,f(2)=1(1)求f(4)、f(1)、f(-1)的值;
(2)求证f(x)为偶函数;
(3)求证f(x)在(0,+
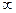 )上是增函数;
)上是增函数;(4)解不等式f(x
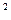 -5)<2.
-5)<2.略
(1)f(4)="2" f(1)="0" f(- 1)="0"
1)="0"
(2)令a=x,b=-1得f(- x)=f(x)+f(-1)即f(-x)=f(x)
x)=f(x)+f(-1)即f(-x)=f(x)
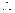 f(x)是偶函数
f(x)是偶函数
(3)设0< <
<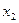 且
且 ,
,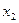 任意令
任意令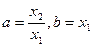 则f(
则f(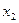 )= f(
)= f(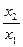 )+f(
)+f( )
)
由0< <
<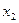 得
得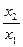 >1
>1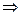 f(
f(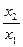 )>0
)>0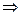 f(
f(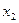 )-f(
)-f( )>0
)>0
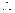 f(x)在(0,+
f(x)在(0,+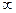 )上是函数
)上是函数
(4)由f(4)="2" 得f(x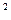 -5)<f(4)
-5)<f(4)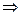 -4<x
-4<x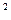 -5<4
-5<4
 不等式f(x
不等式f(x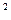 -5)<2的解集为(-3,-1)
-5)<2的解集为(-3,-1)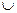 (1,3)
(1,3)
 1)="0"
1)="0" (2)令a=x,b=-1得f(-
 x)=f(x)+f(-1)即f(-x)=f(x)
x)=f(x)+f(-1)即f(-x)=f(x)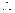 f(x)是偶函数
f(x)是偶函数(3)设0<
 <
<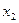 且
且 ,
,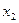 任意令
任意令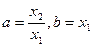 则f(
则f(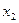 )= f(
)= f(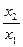 )+f(
)+f( )
)由0<
 <
<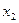 得
得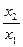 >1
>1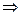 f(
f(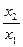 )>0
)>0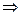 f(
f(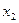 )-f(
)-f( )>0
)>0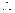 f(x)在(0,+
f(x)在(0,+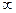 )上是函数
)上是函数(4)由f(4)="2" 得f(x
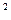 -5)<f(4)
-5)<f(4)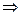 -4<x
-4<x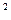 -5<4
-5<4 不等式f(x
不等式f(x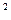 -5)<2的解集为(-3,-1)
-5)<2的解集为(-3,-1) (1,3)
(1,3)
练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 ,若同时满足
,若同时满足 ,使得任取
,使得任取 ,都有
,都有 是常数);
是常数); ,当
,当 时总有
时总有 ,则称
,则称 为“平底型”函数。
为“平底型”函数。 是否是“平底型”函数?简要说明理由;
是否是“平底型”函数?简要说明理由; ,对一切
,对一切 恒成立,求实数
恒成立,求实数 的范围;
的范围; 是“平底型”函数,求
是“平底型”函数,求 和
和 满足的条件,并说明理由。
满足的条件,并说明理由。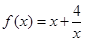 ,
, 的最小值,并确定取得最小值时
的最小值,并确定取得最小值时 的值,列表如下:
的值,列表如下:
 时,
时, 上递减,在区间 上递增;
上递减,在区间 上递增; = 时,
= 时,  时,
时, 在
在 内有两个不相等的实数根,求实数
内有两个不相等的实数根,求实数 的取值范围。
的取值范围。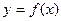 的图象如图①所示,则图②是下列哪个函数的图象( ).刘文迁
的图象如图①所示,则图②是下列哪个函数的图象( ).刘文迁





 对于任意实数
对于任意实数 满足条件
满足条件 ,若
,若 则
则 _______________.
_______________. ,若对任意x1>0,x2>0,均有f(x1+x2)=f(x1)+ f(x2),且f(8)=3,则f(2)=
,若对任意x1>0,x2>0,均有f(x1+x2)=f(x1)+ f(x2),且f(8)=3,则f(2)=
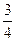

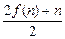 (n∈N*),且f(1)=2,则f(20)为( )
(n∈N*),且f(1)=2,则f(20)为( )
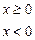 则
则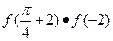 等于
等于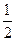 B --
B -- 是定义在R上,且周期为2的偶函数,当
是定义在R上,且周期为2的偶函数,当 。
。 与曲线
与曲线 恰有两个公共点,那么实数
恰有两个公共点,那么实数 的值为()
的值为()



