题目内容
11.在(2$\sqrt{x}$-$\frac{1}{\sqrt{x}}$)6的展开式中,求:(1)第3项的二项式系数及系数.
(2)含x2的项.
分析 (1)由条件利用二项式展开式的通项公式,第r+1项的二项式系数的定义、第r+1项的系数的定义,求得第3项的二项式系数及系数.
(2)先求出二项式展开式的通项公式,再令x的幂指数等于2,求得r的值,即可求得展开式中的含x2的项.
解答 解:(1)第3项的二项式系数为${C}_{6}^{2}$=15,第三项的系数为T3=${C}_{6}^{2}$•24•(-1)2=240.
(2)通项公式为 Tk+1=${C}_{6}^{r}$•26-r•(-1)r•x3-r,令3-r=2,可得r=1,
故含x2的项为第2项,且T2=-192x2.
点评 本题主要考查二项式定理的应用,二项式系数的性质,注意各项系数和与各项的二项式系数和的区别,二项式展开式的通项公式,属于基础题.

练习册系列答案
相关题目
2.不等式(3x+1)(2x-1)>0的解集是( )
| A. | $\{x|x<-\frac{1}{3}或x>\frac{1}{2}\}$ | B. | $\{x|-\frac{1}{3}<x<\frac{1}{2}\}$ | C. | $\{x|x>\frac{1}{2}\}$ | D. | $\{x|x>-\frac{1}{3}\}$ |
6.设a,b是非零实数,且满足$\frac{asin\frac{π}{5}+bcos\frac{π}{5}}{acos\frac{π}{5}-bsin\frac{π}{5}}$=tan$\frac{8π}{15}$,若类比两角和的正切公式,则$\frac{b}{a}$=( )
| A. | 4 | B. | $\sqrt{15}$ | C. | 2 | D. | $\sqrt{3}$ |
16. 如图,阴影部分的面积是( )
如图,阴影部分的面积是( )
 如图,阴影部分的面积是( )
如图,阴影部分的面积是( )| A. | 2$\sqrt{3}$ | B. | -2$\sqrt{3}$ | C. | $\frac{32}{3}$ | D. | $\frac{35}{3}$ |
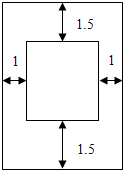 某出版社出版一读物,为了排版设计的需要,规定:一页上所印文字的矩形区域需要占去150cm2,上、下边各要留1.5cm宽的空白,左、右两边各要留1cm宽的空白,出版商为了节约纸张,应选用怎样尺寸的矩形纸张来设计版面?
某出版社出版一读物,为了排版设计的需要,规定:一页上所印文字的矩形区域需要占去150cm2,上、下边各要留1.5cm宽的空白,左、右两边各要留1cm宽的空白,出版商为了节约纸张,应选用怎样尺寸的矩形纸张来设计版面?