题目内容
13．与双曲线x2-$\frac{y^2}{4}$=1有共同的渐近线，且过点（2，2）的双曲线方程为（ ）| A． | $\frac{x^2}{2}$-$\frac{y^2}{8}$=1 | B． | $\frac{x^2}{3}$-$\frac{y^2}{12}$=1 | C． | $\frac{y^2}{3}$-$\frac{x^2}{12}$=1 | D． | $\frac{y^2}{2}$-$\frac{x^2}{8}$=1 |
分析 设双曲线方程为${x^2}-\frac{y^2}{4}=k$，利用双曲线过点（2，2），求出k，即可得出双曲线方程．
解答 解：设双曲线方程为${x^2}-\frac{y^2}{4}=k$．
∵双曲线过点（2，2），∴${2^2}-\frac{2^2}{4}=k$，
∴k=3．
故选：B．
点评 本题考查双曲线方程与性质，考查学生的计算能力，比较基础．
练习册系列答案
科学实验活动册系列答案
相关题目
3．命题p：?x∈R，2x＜3x；命题q：?x∈R，$\sqrt{x}=lo{g}_{\frac{1}{2}}x$，则下列命题中为真命题的是（ ）
| A． | p∧q | B． | ￢p∧q | C． | p∧￢q | D． | ￢p∧￢q |
4．
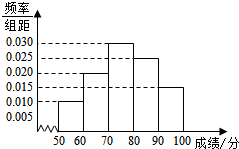对某次联考数学成绩（百分制）进行分析，如图为分析结果的频率分布直方图．根据标准，成绩分数在区间[50，60）上为不及格，在[60，70）上为一般，在[70，80）上为较好，在[80，90）上为良好，在[90，100]上为优秀．用频率估计概率，若从参考学生中随机抽取1人，则其成绩为优良（优秀或良好）的概率为（ ）
对某次联考数学成绩（百分制）进行分析，如图为分析结果的频率分布直方图．根据标准，成绩分数在区间[50，60）上为不及格，在[60，70）上为一般，在[70，80）上为较好，在[80，90）上为良好，在[90，100]上为优秀．用频率估计概率，若从参考学生中随机抽取1人，则其成绩为优良（优秀或良好）的概率为（ ）| A． | 0.09 | B． | 0.20 | C． | 0.25 | D． | 0.40 |
8．已知圆C1：（x-3）2+（y+1）2=1，圆C2与圆C1关于直线2x-y-2=0对称，则圆C2的方程为（ ）
| A． | （x-1）2+（y-2）2=1 | B． | x2+（y-1）2=1 | C． | （x+1）2+（y-1）2=1 | D． | （x+2）2+（y-1）2=1 |
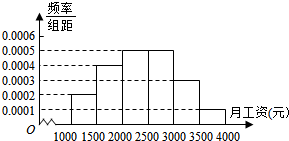进入2014年金秋，新入职的大学生陆续拿到了第一份薪水．某地调查机构就月薪情况调查了1000名新入职大学生，并根据所得数据画出样本的频率分布直方图（每个分组包括左端点，不包括右端点，如第一组表示月薪在[1000，1500）单位：元）．