题目内容
6.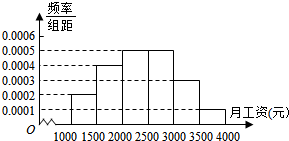 进入2014年金秋,新入职的大学生陆续拿到了第一份薪水.某地调查机构就月薪情况调查了1000名新入职大学生,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月薪在[1000,1500)单位:元).
进入2014年金秋,新入职的大学生陆续拿到了第一份薪水.某地调查机构就月薪情况调查了1000名新入职大学生,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月薪在[1000,1500)单位:元).(Ⅰ)求新入职大学生的月薪在[3000,4000)的频率,并根据频率分布直方图估计出样本数据的中位数;
(Ⅱ)为了分析新入职大学生的月薪与其性别的关系,必须按月薪再从这 1000人中按分层抽样方法抽出100人作进一步分析,已知月薪在[3500,4000)的被抽取出的人中恰有2位女性.若从月薪在[3500,4000)的被抽取出的人随机选出2人填写某项调查问卷,求这2人中至少有一位男性的概率.
分析 (Ⅰ)根据频率分布直方图可知[3000,4000)的频率,确定中位数;
(2)根据分层抽样,求出所抽取的人数,记3位男性为a1、a2、a3,2位女性为b1、b2.列举出所有的基本事件,根据概率公式计算即可.
解答 解:(Ⅰ)新入职大学生的月薪在[3000,4000)的频率为(0.0003+0.0001)×500=0.2,
估计中位数x为0.0002×500+0.0004×500+0.0005×(x-2000)=0.5
解得x=2400;
(Ⅱ)依题意,月薪在[3500,4000)的被抽取出$1000×0.0001×500×\frac{100}{1000}=5$人,且恰有2位女性.记3位男性为a1、a2、a3,2位女性为b1、b2.从这5人中抽取2人的所有取法有:(a1,a2)、(a1,a3)、(a1,b1)、(a1,b2),(a2,a3)、(a2,b1)、(a2,b2),(a3,b1)、(a3,b2)、(b1,b2)共10种.
记事件A=“2人中至少有一位男性“,则事件A含9个基本事件,
故$P(A)=\frac{9}{10}$.
点评 本题考查二类频率分布直方图和古典概型的概率问题,不重不漏的列举是关键,属于基础题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
12.学校开设美术、舞蹈、计算机三门选修课,现有四名同学参与选课,且每人限选一门课程,那么不同的选课方法的种数是( )
| A. | 12 | B. | 24 | C. | 64 | D. | 81 |
13.与双曲线x2-$\frac{y^2}{4}$=1有共同的渐近线,且过点(2,2)的双曲线方程为( )
| A. | $\frac{x^2}{2}$-$\frac{y^2}{8}$=1 | B. | $\frac{x^2}{3}$-$\frac{y^2}{12}$=1 | C. | $\frac{y^2}{3}$-$\frac{x^2}{12}$=1 | D. | $\frac{y^2}{2}$-$\frac{x^2}{8}$=1 |
1.先后抛掷两枚均匀的骰子,骰子点数分别记为x,y,则log2xy>1的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{5}{36}$ | C. | $\frac{7}{36}$ | D. | $\frac{5}{12}$ |
11.角α终边上有一点(-a,2a)(a<0),则sinα=( )
| A. | -$\frac{2\sqrt{5}}{5}$ | B. | -$\frac{\sqrt{5}}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |