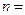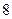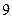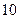题目内容
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
在数列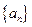 中,
中,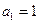 ,
,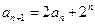 .
.
(1)设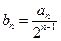
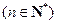 ,证明:数列
,证明:数列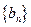 是等差数列;
是等差数列;
(2)设 数列
数列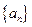 的前
的前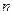 项和为
项和为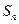 ,求
,求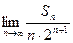 的值;
的值;
(3)设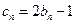 ,数列
,数列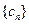 的前
的前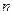 项和为
项和为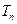 ,
,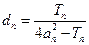 ,是否存在
,是否存在 实数
实数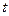 ,使得对任意的正整数
,使得对任意的正整数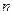 和实数
和实数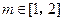 ,都有
,都有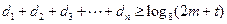 成立?请说明理由.
成立?请说明理由.
在数列
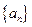 中,
中,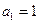 ,
,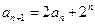 .
.(1)设
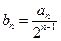
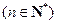 ,证明:数列
,证明:数列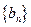 是等差数列;
是等差数列;(2)设
 数列
数列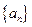 的前
的前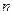 项和为
项和为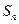 ,求
,求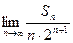 的值;
的值;(3)设
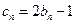 ,数列
,数列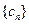 的前
的前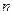 项和为
项和为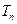 ,
,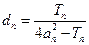 ,是否存在
,是否存在 实数
实数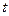 ,使得对任意的正整数
,使得对任意的正整数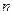 和实数
和实数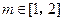 ,都有
,都有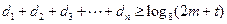 成立?请说明理由.
成立?请说明理由.略
(1)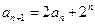 ,
,
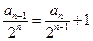 , (2分)
, (2分)
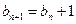 , 故
, 故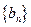 为等差数列,
为等差数列,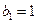 ,
,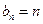 . (4分)
. (4分)
(2)由(1)可得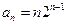 (6分)
(6分) 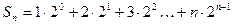

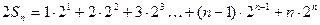
两式相减,得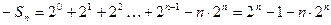 ,即
,即
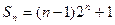 (8分)
(8分) 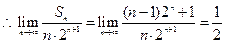 (10分)
(10分)
(3)由(1)可得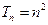 ,(12分) ∴
,(12分) ∴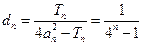 ,
,
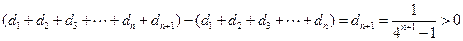
∴
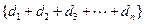 单调递增,即
单调递增,即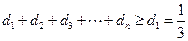 , (14分)要使
, (14分)要使
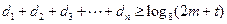 对任意正整数
对任意正整数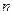 成立,
成立,
必须且只需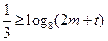 ,即
,即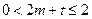 对任意
对任意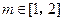 恒成立.(16分)∴
恒成立.(16分)∴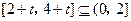 ,即
,即 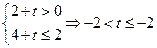 矛盾.
矛盾.
∴满足条件的实数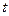 不存在. (18分)
不存在. (18分)
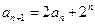 ,
,
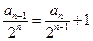 , (2分)
, (2分)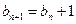 , 故
, 故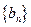 为等差数列,
为等差数列,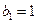 ,
,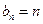 . (4分)
. (4分)(2)由(1)可得
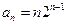 (6分)
(6分) 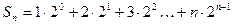

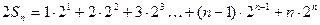
两式相减,得
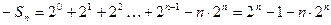 ,即
,即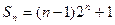 (8分)
(8分) 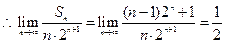 (10分)
(10分)(3)由(1)可得
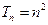 ,(12分) ∴
,(12分) ∴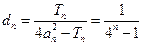 ,
,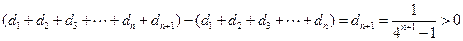
∴

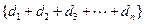 单调递增,即
单调递增,即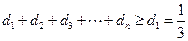 , (14分)要使
, (14分)要使
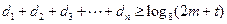 对任意正整数
对任意正整数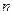 成立,
成立,必须且只需
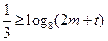 ,即
,即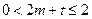 对任意
对任意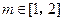 恒成立.(16分)∴
恒成立.(16分)∴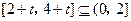 ,即
,即 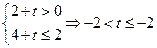 矛盾.
矛盾.∴满足条件的实数
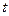 不存在. (18分)
不存在. (18分)
练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
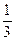 )是函数
)是函数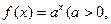 且
且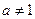 )的图象上一点,等比数列
)的图象上一点,等比数列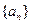 的前
的前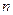 项和为
项和为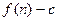 ,数列
,数列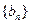
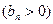 的首项为
的首项为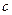 ,且前
,且前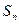 满足
满足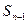 =
=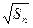 +
+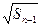 (
(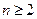 ).
).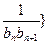 前
前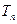 ,问
,问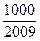 的最小正整数
的最小正整数

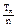 ,若a=2
,若a=2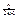 ,求满足不等式
,求满足不等式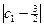 +
+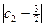 +…+
+…+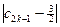 +
+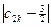 ≥
≥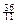 时k的最小值.
时k的最小值.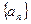 中,
中,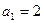 ,点
,点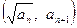 在函数
在函数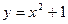 的图像上,数列
的图像上,数列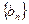 中,点
中,点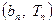 在直线
在直线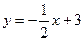 上,其中
上,其中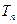 是数列
是数列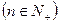 。
。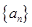 是等差数列,
是等差数列,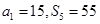 ,则过点
,则过点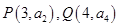 的直线斜率为
的直线斜率为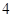
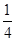
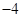
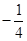
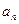 }的首项为
}的首项为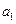 =
=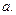 公比为q,则
公比为q,则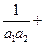
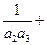 …
…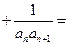 __________。
__________。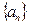 中,已知
中,已知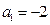 ,
,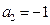 ,
,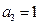 ,若对任意正整数
,若对任意正整数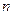 ,有
,有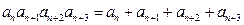 ,且
,且
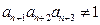 ,则该数列的前2010 项和
,则该数列的前2010 项和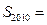 ( )
( )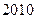 .
.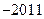 .
.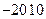 .
.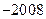 .
.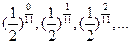 ,则使这个数列前
,则使这个数列前 项的积不小于
项的积不小于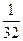 的最大正数
的最大正数