题目内容
数列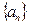 中,已知
中,已知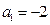 ,
,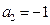 ,
,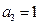 ,若对任意正整数
,若对任意正整数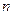 ,有
,有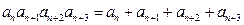 ,且
,且
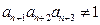 ,则该数列的前2010 项和
,则该数列的前2010 项和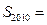 ( )
( )
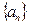 中,已知
中,已知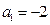 ,
,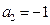 ,
,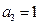 ,若对任意正整数
,若对任意正整数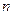 ,有
,有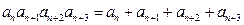 ,且
,且
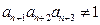 ,则该数列的前2010 项和
,则该数列的前2010 项和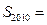 ( )
( )A.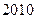 . . | B.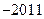 . . | C.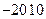 . . | D.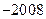 . . |
B
略

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
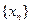 满足
满足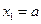 ,
,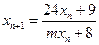
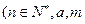 是实数).
是实数).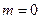 ,
,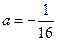 ,求通项
,求通项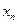 ;
;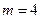 ,设数列
,设数列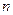 项和当
项和当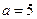 时为
时为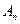 ,当
,当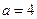 时为
时为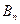 ,
,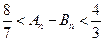
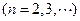 .
.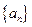 中,
中,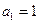 ,
,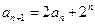 .
.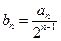
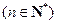 ,证明:数列
,证明:数列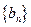 是等差数列;
是等差数列; 数列
数列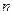 项和为
项和为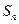 ,求
,求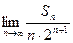 的值;
的值;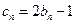 ,数列
,数列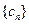 的前
的前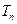 ,
,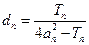 ,是否存在
,是否存在 实数
实数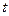 ,使得对任意的正整数
,使得对任意的正整数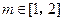 ,都有
,都有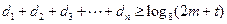 成立?请说明理由.
成立?请说明理由.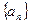 满足
满足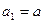 ,
,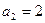 ,
,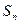 是数列的前
是数列的前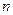 项和,且
项和,且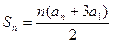 (
(
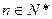 ).
).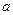 的值;
的值; 列
列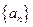 的通项公式;
的通项公式; (3)对于数列
(3)对于数列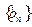 ,若存在常数M,使
,若存在常数M,使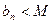 (
(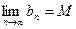 ,则M叫做数列
,则M叫做数列 (
(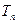 为数列
为数列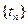 的前
的前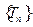 的上渐近值.
的上渐近值.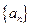 为等差数列,且
为等差数列,且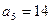 ,
, ,数列
,数列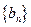 的前
的前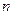 项和为
项和为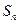 ,
,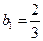 且
且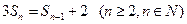 ;,
;,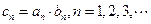 ,
,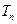 为数列
为数列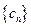 的前
的前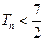 .
.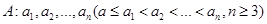 具有性质P:对任意
具有性质P:对任意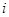 ,
,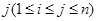 ,
,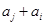 与
与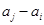 两数中至少有一个是该数列中的一项,现给出以下四个命题:
两数中至少有一个是该数列中的一项,现给出以下四个命题: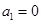 ;
;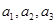
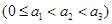 具有性质P,则
具有性质P,则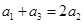
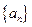 中,
中,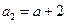 (
(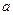 为常数),
为常数),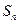 为
为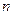 项和,且
项和,且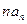 与
与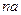 的等差中项.
的等差中项.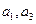 ;
;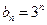 且
且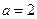 ,
,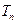 为数列
为数列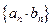 的前
的前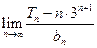 的值.
的值.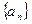 中,
中,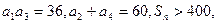 求
求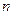 的范围.
的范围.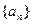 中,
中,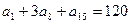 ,则
,则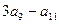 的值为多少?
的值为多少?