题目内容
(本小题满分14分)
已知:有穷数列{an}共有2k项(整数k≥2 ),a1="2" ,设该数列的前n项和为 Sn且满足Sn+1=aSn+2(n=1,2,…,2k-1),a>1.
(1)求{an}的通项公式;
(2)设bn=log2an,求{bn}的前n项和Tn;
(3)设cn=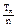 ,若a=2
,若a=2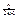 ,求满足不等式
,求满足不等式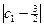 +
+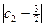 +…+
+…+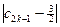 +
+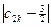 ≥
≥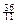 时k的最小值.
时k的最小值.
已知:有穷数列{an}共有2k项(整数k≥2 ),a1="2" ,设该数列的前n项和为 Sn且满足Sn+1=aSn+2(n=1,2,…,2k-1),a>1.
(1)求{an}的通项公式;
(2)设bn=log2an,求{bn}的前n项和Tn;
(3)设cn=
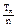 ,若a=2
,若a=2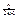 ,求满足不等式
,求满足不等式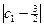 +
+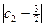 +…+
+…+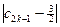 +
+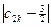 ≥
≥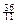 时k的最小值.
时k的最小值.(1)an=2·an-1(n=1,2…,2k);(2)Tn=n+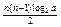 (a>1,n=1,2,…,2k)(3)k≥6或k≤
(a>1,n=1,2,…,2k)(3)k≥6或k≤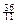
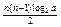 (a>1,n=1,2,…,2k)(3)k≥6或k≤
(a>1,n=1,2,…,2k)(3)k≥6或k≤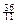
(1)由Sn+1=aSn+2(n=1,2,…,2k-1) (1)
Sn=aSn-1+2(n=2,3,…,k) (2)……………………………2分
(1)-(2)得an+1=a·an(n=2,3,…,2k-1)
由(1)式S2=aS1+2,a1+a2=aS1+2……………………………………………………3分
解得a2=2a,因为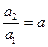
所以{an}是以2为首项,a为公比的等比数列,an=2·an-1(n=1,2…,2k)…………4分
(2)∵bn-bn-1=log2an-log2an-1=log2an-1log2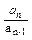 =log2a (n=2,3…,2k)
=log2a (n=2,3…,2k)
∴{bn}是以b1=1为首项,以log2a(a>1)为公差的等差数列………………………6分
∴Tn=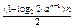 =
=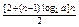 =n+
=n+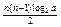 (a>1,n=1,2,…,2k)……………8分
(a>1,n=1,2,…,2k)……………8分
(3)cn=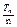 =1+
=1+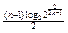 =1+
=1+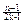 (n=1,2,…,2k)……………………………10分
(n=1,2,…,2k)……………………………10分
当cn≤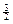 时, n≤k+
时, n≤k+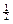 ,n为正整数,知n≤k时,cn<
,n为正整数,知n≤k时,cn<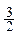
当n≥k+1时,cn>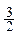 ……………………………………………………………………11分
……………………………………………………………………11分
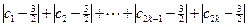
=(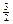 -c1)+(
-c1)+(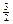 -c2)+…+(
-c2)+…+(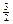 -ck)+(ck+1-
-ck)+(ck+1-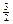 )+…+(c2
)+…+(c2 k-
k-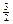 )
)
=(ck+1+ck+2+…+c2k)-(c1+c2+…+ck)
=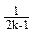 {[k+(k+1)+…+(2k-1)]+2k}-
{[k+(k+1)+…+(2k-1)]+2k}-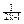 {[1+2+…+(k-1)]+k}
{[1+2+…+(k-1)]+k}
=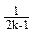 [
[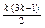 -
-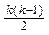 ]
]
=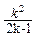 ≥
≥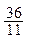
即11k2-72k+3 6≥0,(11k-6)(k-6)≥0解得k≥6或k≤
6≥0,(11k-6)(k-6)≥0解得k≥6或k≤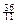
所以满足条件的k的最小值为6…………………………14分
Sn=aSn-1+2(n=2,3,…,k) (2)……………………………2分
(1)-(2)得an+1=a·an(n=2,3,…,2k-1)
由(1)式S2=aS1+2,a1+a2=aS1+2……………………………………………………3分
解得a2=2a,因为
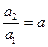
所以{an}是以2为首项,a为公比的等比数列,an=2·an-1(n=1,2…,2k)…………4分
(2)∵bn-bn-1=log2an-log2an-1=log2an-1log2
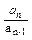 =log2a (n=2,3…,2k)
=log2a (n=2,3…,2k)∴{bn}是以b1=1为首项,以log2a(a>1)为公差的等差数列………………………6分
∴Tn=
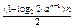 =
=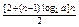 =n+
=n+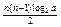 (a>1,n=1,2,…,2k)……………8分
(a>1,n=1,2,…,2k)……………8分(3)cn=
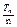 =1+
=1+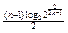 =1+
=1+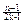 (n=1,2,…,2k)……………………………10分
(n=1,2,…,2k)……………………………10分当cn≤
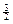 时, n≤k+
时, n≤k+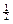 ,n为正整数,知n≤k时,cn<
,n为正整数,知n≤k时,cn<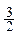
当n≥k+1时,cn>
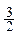 ……………………………………………………………………11分
……………………………………………………………………11分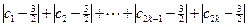
=(
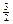 -c1)+(
-c1)+(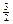 -c2)+…+(
-c2)+…+(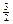 -ck)+(ck+1-
-ck)+(ck+1-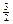 )+…+(c2
)+…+(c2 k-
k-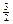 )
)=(ck+1+ck+2+…+c2k)-(c1+c2+…+ck)
=
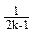 {[k+(k+1)+…+(2k-1)]+2k}-
{[k+(k+1)+…+(2k-1)]+2k}-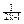 {[1+2+…+(k-1)]+k}
{[1+2+…+(k-1)]+k}=
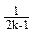 [
[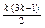 -
-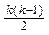 ]
]=
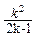 ≥
≥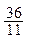
即11k2-72k+3
 6≥0,(11k-6)(k-6)≥0解得k≥6或k≤
6≥0,(11k-6)(k-6)≥0解得k≥6或k≤
所以满足条件的k的最小值为6…………………………14分

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
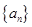 中有两项
中有两项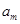 和
和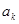 ,满足
,满足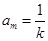 、
、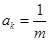 ,则该数列前mk项之和是
,则该数列前mk项之和是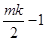
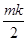
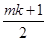
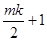
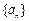 中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列
中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列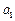 、公差为
、公差为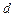

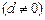 的无穷等差数列.
的无穷等差数列.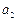 ,
,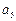 成等比数列,求其公比
成等比数列,求其公比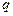 .
.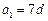 ,从数列
,从数列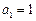 ,从数列
,从数列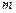
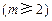 项(设
项(设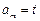 )作为一个等比数列的第1项、第2项.求证:当
)作为一个等比数列的第1项、第2项.求证:当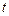 为大于1的正整数时,该数列为
为大于1的正整数时,该数列为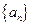 的首项为1,前
的首项为1,前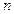 项和为
项和为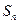 ,且满足
,且满足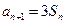 ,
,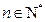 .数列
.数列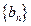 满足
满足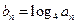 .
. 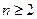 时,试比较
时,试比较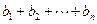 与
与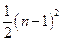 的大小,并说明理由;
的大小,并说明理由;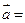
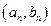 是否可能恰为直线
是否可能恰为直线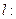
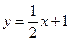 的方向向量?请说明你的理由.
的方向向量?请说明你的理由.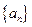 中,
中,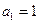 ,
,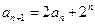 .
.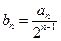
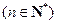 ,证明:数列
,证明:数列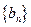 是等差数列;
是等差数列; 数列
数列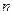 项和为
项和为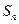 ,求
,求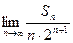 的值;
的值;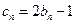 ,数列
,数列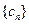 的前
的前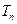 ,
,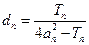 ,是否存在
,是否存在 实数
实数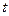 ,使得对任意的正整数
,使得对任意的正整数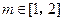 ,都有
,都有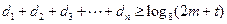 成立?请说明理由.
成立?请说明理由.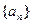 满足:
满足: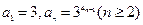 .
.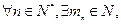 使
使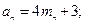
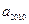 的末位数字.
的末位数字.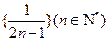 的所有项按照从大到小的原则写成如右图所示的数表,其中的第
的所有项按照从大到小的原则写成如右图所示的数表,其中的第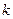 行有
行有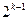 个数,第
个数,第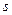 个数(从左数起)记为
个数(从左数起)记为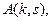 则
则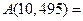

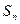 为等差数列
为等差数列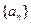 的前
的前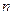 项和,若
项和,若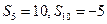 ,则数列
,则数列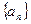 中,公差
中,公差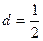 ,前
,前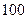 项的和
项的和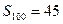 ,则
,则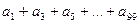 的值为( ).
的值为( ).