Question

【题目】对定义在[0，1]上，并且同时满足以下两个条件的函数f（x）称为M函数：
（i）对任意的x∈[0，1]，恒有f（x）≥0；
（ii）当x1≥0，x2≥0，x1+x2≤1时，总有f（x1+x2）≥f（x1）+f（x2）成立．
则下列四个函数中不是M函数的个数是（ ）
①f（x）=x2②f（x）=x2+1
③f（x）=ln（x2+1）④f（x）=2x﹣1．
A.1
B.2
C.3
D.4

Answer 1

【答案】A
【解析】解：（i）在[0，1]上，四个函数都满足；（ii）x1≥0，x2≥0，x1+x2≤1；
对于①， ，∴①满足；
对于②， =2x1x2﹣1＜0，∴②不满足．
对于③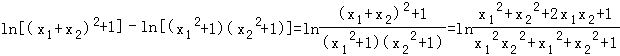， = 而x1≥0，x2≥0，∴ ，∴ ，∴ ，
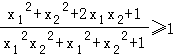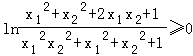∴ ，∴ ，∴③满足；
对于④，
= ，∴④满足；
故选：A．