题目内容
【题目】已知幂函数f（x）=xa的图象经过点（ 
， 
）．
（1）求函数f（x）的解析式，并判断奇偶性；
（2）判断函数f（x）在（﹣∞，0）上的单调性，并用单调性定义证明．
（3）作出函数f（x）在定义域内的大致图象（不必写出作图过程）．
【答案】
（1）解：依题得： 
= 
，m=﹣2．
故f（x）=x﹣2．
f（﹣x）=（﹣x）﹣2= 
=x﹣2=f（x），
所以，f（x）是偶函数
（2）解：假设任意x1＜x2＜0
f（x1）﹣f（x2）=x1﹣2﹣x2﹣2= 
= 
＜0，
∴f（x1）＜f（x2）
∴f（x）在（﹣∞，0）上是增函数
（3）解：如图．
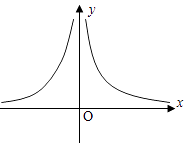
【解析】（1）利用幂函数经过的点，求解函数的解析式，利用奇偶性的定义判断即可．（2）利用函数单调性的定义证明即可；（3）画出函数的图象即可．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
