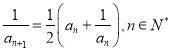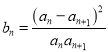题目内容
【题目】已知函数f(x)是定义在R上不恒为0的函数,且对于任意的实数a,b满足f(2)=2,f(ab)=af(b)+bf(a),an= ![]() (n∈N*),bn=
(n∈N*),bn= ![]() (n∈N*),给出下列命题:
(n∈N*),给出下列命题:
①f(0)=f(1);
②f(x)为奇函数;
③数列{an}为等差数列;
④数列{bn}为等比数列.
其中正确的命题是 . (写出所有正确命题的序号)
【答案】①②③④
【解析】解:∵取a=b=0,可得f(0)=0,
取a=b=1,可得f(1)=2f(1),即f(1)=0,
∴f(0)=f(1),
即①正确;
令a=b=﹣1,则f(1)=﹣f(﹣1)﹣f(﹣1)=0f(﹣1)=0,
令a=﹣1,则f(﹣b)=﹣f(b)+bf(﹣1)=﹣f(b)f(x)为奇函数,
即②正确;
∵f(ab)=af(b)+bf(a),
∴f(2n)=f(22n﹣1)=2f(2n﹣1)+2n﹣1f(2)
=2f(2n﹣1)+2n=…=n2n ,
∴an= ![]() =n,bn=
=n,bn= ![]() =2n ,
=2n ,
即有③④正确.
所以答案是:①②③④.
【考点精析】通过灵活运用数列的通项公式,掌握如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.

练习册系列答案
相关题目