题目内容
【题目】如图,在底面为矩形的四棱锥![]() 中,
中, ![]() .
.
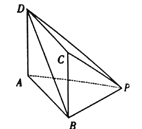
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若异面直线![]() 与
与![]() 所成角为
所成角为![]() ,
, ![]() ,
, ![]() ,求二面角
,求二面角![]() 的大小.
的大小.
【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:
(1)由题意结合几何关系可证得![]() 平面
平面![]() ,结合面面垂直的判断定理即可证得平面
,结合面面垂直的判断定理即可证得平面![]() 平面
平面![]() .
.
(2)建立空间直角坐标系,结合半平面的法向量可得二面角![]() 的大小是
的大小是![]() .
.
试题解析:
(1)证明:由已知四边形![]() 为矩形,得
为矩形,得![]() ,
,
∵![]() ,
, ![]() ,∴
,∴![]() 平面
平面![]() .
.
又![]() ,∴
,∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(2)解:以![]() 为坐标原点,建立如图所示的空间直角坐标系
为坐标原点,建立如图所示的空间直角坐标系![]() .
.
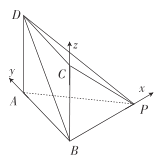
设![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,则
,则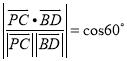 ,即
,即![]() ,
,
解得![]() (
(![]() 舍去).
舍去).
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则![]() ,即
,即![]() ,
,
可取![]() .
.
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则![]() 即
即![]() ,
,
可取![]() ,所以
,所以![]() ,
,
由图可知二面角![]() 为锐角,所以二面角
为锐角,所以二面角![]() 的大小为
的大小为![]() .
.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
【题目】某种产品的广告费支出x与销售额y(单位:万元)之间有如表对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)求广告费支出x与销售额y回归直线方程 ![]() =bx+a(a,b∈R);
=bx+a(a,b∈R);
已知b= 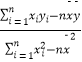 ,
, ![]()
(2)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率.