题目内容
【题目】已知抛物线
的经过点
．
（1）求抛物线的方程；
（2）过抛物线焦点F的直线l交抛物线于A、B两点，若|AB|＝8，求直线l的方程．
【答案】（1）
；（2）
或
．
【解析】
（1）利用
点坐标，求得
的值，进而求得抛物线方程.
（2）由（1）求得
点的坐标.当
与
轴垂直时，求得
；当直线与轴不垂直时，设出直线的方程，与抛物线方程联立，写出韦达定理，根据抛物线的弦长公式列方程，解方程求得直线的斜率，从而求得直线的方程.
（1）把点
带入方程
得
，
所以，抛物线方程为．
（2）抛物线方程得焦点坐标为F（1，0 ），
若直线l与x轴垂直，易得A（1，2 ），B（1，－2 ），此时|AB|≠8．
若直线l不与x轴垂直，设直线l的斜率为k，
则直线l的方程为
．
由
消y整理得：
，
∴ 
．
∴ 
，解得
，即
．
∴直线的方程为
或
，即或．
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
快乐暑假暑假能力自测中西书局系列答案
【题目】近年来，随着我国汽车消费水平的提高，二手车流通行业得到迅猛发展．某汽车交易市场对2017年成交的二手车交易前的使用时间（以下简称“使用时间”）进行统计，得到频率分布直方图如图1．
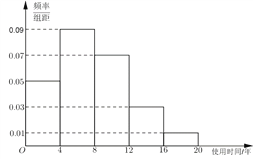
图1 图2
（1）记“在
年成交的二手车中随机选取一辆，该车的使用年限在
”为事件
，试估计的概率；
（2）根据该汽车交易市场的历史资料，得到散点图如图2，其中
(单位：年)表示二手车的使用时间，
(单位：万元)表示相应的二手车的平均交易价格．由散点图看出，可采用
作为二手车平均交易价格关于其使用年限的回归方程，相关数据如下表（表中
，
）：
|
|
|
|
|
|
5.5 | 8.7 | 1.9 | 301.4 | 79.75 | 385 |
①根据回归方程类型及表中数据，建立关于的回归方程；
②该汽车交易市场对使用8年以内(含8年)的二手车收取成交价格
的佣金，对使用时间8年以上(不含8年)的二手车收取成交价格
的佣金．在图1对使用时间的分组中，以各组的区间中点值代表该组的各个值．若以2017年的数据作为决策依据，计算该汽车交易市场对成交的每辆车收取的平均佣金．
附注：①对于一组数据
，其回归直线
的斜率和截距的最小二乘估计分别为
；
②参考数据：
．
