题目内容
【题目】如图,CM,CN为某公园景观湖胖的两条木栈道,∠MCN=120°,现拟在两条木栈道的A,B处设置观景台,记BC=a,AC=b,AB=c(单位:百米)
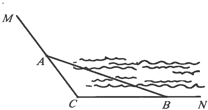
(1)若a,b,c成等差数列,且公差为4,求b的值;
(2)已知AB=12,记∠ABC=θ,试用θ表示观景路线A-C-B的长,并求观景路线A-C-B长的最大值.
【答案】(1)10;(2)8![]() .
.
【解析】
(1)利用a、b、c成等差数列,且公差为4,可得![]() ,利用余弦定理即可求b的值;
,利用余弦定理即可求b的值;
(2)利用正弦定理,求出AC、BC,可得到观景路线A-C-B为![]() 是关于
是关于![]() 的函数,求出最大值即可
的函数,求出最大值即可
解:(1)∵a、b、c成等差数列,且公差为4,∴![]() ,
,
∵∠MCN=120°,
∴![]() ,即
,即![]() °,
°,
∴b=10
(2)由题意,在![]() 中,
中,![]() ,
,
则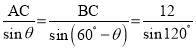 ,
,
∴![]() ,
,![]() ,
,
∴观景路线A-C-B的长![]() ,且
,且![]() ,
,
∴θ=30°时,观景路线A-C-B长的最大值为8![]()

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案【题目】孝感市旅游局为了了解双峰山景点在大众中的熟知度,从年龄在15~65岁的人群中随机抽取n人进行问卷调查,把这n人按年龄分成5组:第一组[15,25),第二组[25,35),第三组[35,45),第四组[45,55),第五组[55,65],得到的样本的频率分布直方图如右:

调查问题是“双峰山国家森林公园是几A级旅游景点?”每组中回答正确的人数及回答正确的人数占本组的频率的统计结果如下表.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第1组 | [15,25) | 5 | 0.5 |
第2组 | [25,35) | 18 | x |
第3组 | [35,45) | y | 0.9 |
第4组 | [45,55) | 9 | a |
第5组 | [55,65] | 7 | b |
(1)分别求出n,x,y的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人;
(3)在(2)抽取的6人中随机抽取2人,求所抽取的两人来自不同年龄组的概率.

