题目内容
12．关于x的不等式ax2-5x+b＜0的解集是（2，3），则a+b的值等于7．分析 根据一元二次不等式与对应方程之间的关系，得出方程的两个根为2和3，
再利用根与系数的关系求出a、b的值即可．
解答 解：∵关于x的不等式ax2-5x+b＜0的解集是（2，3），
∴关于x的方程ax2-5x+b=0的两个根为2和3，
∴$\frac{5}{a}$=2+3，$\frac{b}{a}$=2×3；
解得a=1，b=6；
∴a+b=1+6=7．
故答案为：7．
点评 本题考查了一元二次不等式与对应方程之间的关系应用问题，也考查了根与系数的应用问题，是基础题目．
练习册系列答案
阅读快车系列答案
相关题目
2．等比数列{an}满足a2+8a5=0，设Sn是数列{$\frac{1}{{a}_{n}}$}的前n项和，则$\frac{{S}_{5}}{{S}_{2}}$=（ ）
| A． | -11 | B． | -8 | C． | 5 | D． | 11 |
3．某几何体的三视图如图所示，则该几何体的体积为（ ）
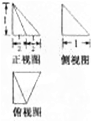
| A． | 1 | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{4}$ |
20．某校组织一次校外活动，有10名同学参加，其中有6名男生，4名女生，从中随机抽取3名，其中至多有1名女生的概率（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{5}{6}$ |
7．已知函数$f（x）=\left\{\begin{array}{l}{log_x}4，x＞0\\{2^{kx-1}}，x≤0\end{array}\right.$，若f（2）=f（-2），则k=（ ）
| A． | 1 | B． | -1 | C． | 2 | D． | -2 |
1．i为虚数单位，复数$\frac{{3i-{i^{2014}}}}{1-i}$的化简结果为（ ）
| A． | 2+i | B． | 1+2i | C． | -1+2i | D． | -2+i |
17．
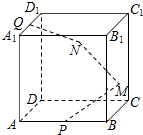如图，在边长为2的正方体ABCD-A1B1C1D1中，P、Q分别为棱AB、A1D1的中点，M、N分别为面BCC1B1和DCC1D1上的点，一质点从点P射向点M，遇正方体的面反射（反射服从光的反射原理），反射到点N，再经平面反射，恰好反射至点Q，则三条线段PM、MN、NQ的长度之和为（ ）
如图，在边长为2的正方体ABCD-A1B1C1D1中，P、Q分别为棱AB、A1D1的中点，M、N分别为面BCC1B1和DCC1D1上的点，一质点从点P射向点M，遇正方体的面反射（反射服从光的反射原理），反射到点N，再经平面反射，恰好反射至点Q，则三条线段PM、MN、NQ的长度之和为（ ）| A． | $\sqrt{22}$ | B． | $\sqrt{21}$ | C． | 2$\sqrt{5}$ | D． | 3$\sqrt{2}$ |