题目内容
17．
如图，在边长为2的正方体ABCD-A1B1C1D1中，P、Q分别为棱AB、A1D1的中点，M、N分别为面BCC1B1和DCC1D1上的点，一质点从点P射向点M，遇正方体的面反射（反射服从光的反射原理），反射到点N，再经平面反射，恰好反射至点Q，则三条线段PM、MN、NQ的长度之和为（ ）| A． | $\sqrt{22}$ | B． | $\sqrt{21}$ | C． | 2$\sqrt{5}$ | D． | 3$\sqrt{2}$ |
分析 作点P关于平面BCC1B1的对称点P1，再作Q关于平面DCC1D1的对称点Q1，连接P1Q1，根据勾股定理即可求得长度之和．
解答 
解：作点P关于平面BCC1B1的对称点P1，再作Q关于平面DCC1D1的对称点Q1，连接P1Q1，这就是光线所经过的等效路径，
其长度就是PM，MN，NQ三条线段的长度之和，
根据勾股定理：|P1Q1|2=（A1Q1）2+（AA1）2+（AP1）2=32+22+32=22，
可得|P1Q1|=$\sqrt{22}$，
故选：A．
点评 本题考查了正方体的几何性质，光的反射原理，对称性问题，化折线为直线求解线段的长度，题目很新颖，属于中档题．
练习册系列答案
全能练考卷系列答案
一课一练课时达标系列答案
相关题目
5．对于平面α、β和直线a、b，若a?α，b?β，α∥β，则直线a、b不可能是（ ）
| A． | 相交 | B． | 平行 | C． | 异面 | D． | 垂直 |
2．下列运算结果中，正确的是（ ）
| A． | a2a3=a5 | B． | （-a2）3=（-a3）2 | C． | （$\sqrt{a}$-1）0=1 | D． | （-a2）3=a6 |
6．已知某中学高三文科班学生共有800人参加了数学与地理的水平测试，学校决定利用随机数表法从中抽取100人进行成绩抽样调查，先将800人按001、002、…800编号．
（1）下面摘取了随机数表的第7行到第9行
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 67 19 98 10 66 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
如果从第8行第7列的数开始向右读，请你依次写出最先检查的5个人的编号；
（2）抽取的100人的数学与地理的水平测试成绩如下表：
成绩分为优秀、良好、及格三个等级；横向、纵向分别表示地理成绩与数学成绩各等级人数，例如：表中数学成绩为良好的共有20+18+4=42．在该样本中，数学成绩优秀率是30%，
在地理成绩及格的学生中，已知a≥10，b≥8，求数学成绩优秀的人数比及格的人数少的概率．
（1）下面摘取了随机数表的第7行到第9行
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 67 19 98 10 66 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
如果从第8行第7列的数开始向右读，请你依次写出最先检查的5个人的编号；
（2）抽取的100人的数学与地理的水平测试成绩如下表：
成绩分为优秀、良好、及格三个等级；横向、纵向分别表示地理成绩与数学成绩各等级人数，例如：表中数学成绩为良好的共有20+18+4=42．在该样本中，数学成绩优秀率是30%，
| 人数 | 数学 | |||
| 优秀 | 良好 | 及格 | ||
地 理 | 优秀 | 7 | 20 | 5 |
| 良好 | 9 | 18 | 6 | |
| 及格 | a | 4 | b | |
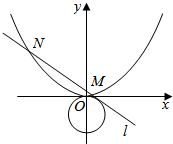已知抛物线的顶点在坐标原点，焦点在y轴上，且过点（2，1）．