题目内容
4.某几何体的三视图及部分数据如图所示,则此几何体的表面积是$3+4\sqrt{3}$.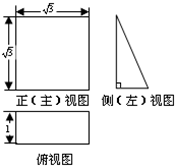
分析 几何体是直三棱柱,根据三视图判断三棱柱的侧棱长、底面三角形的形状及相关几何量的数据,把数据直三棱柱的表面积公式计算.
解答 解:由三视图知:几何体是直三棱柱,三棱柱的侧棱长为$\sqrt{3}$,
底面是直角边长分别为$\sqrt{3}$、1的直角三角形,斜边长为2,
∴几何体的表面积S=2×$\frac{1}{2}$×$\sqrt{3}$×1+(1+2+$\sqrt{3}$)×$\sqrt{3}$=$\sqrt{3}$+3$\sqrt{3}$+3=$3+4\sqrt{3}$.
故答案为:$3+4\sqrt{3}$.
点评 本题考查了由三视图求几何体的表面积,根据三视图判断几何体的形状及数据所对应的几何量是关键.

练习册系列答案
相关题目
14.某几何体的三视图如图所示,该几何体的体积为( )
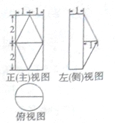

| A. | $\frac{16}{3}$ | B. | 5+$\frac{π}{3}$ | C. | $\frac{7π}{3}$ | D. | $\frac{8π}{3}$ |
9.某商店对每天进店人数x与某种商品成交量y(单位:件)进行了统计,得到如下对应数据:
由表中数据,得线性回归方程为$\hat y=\hat bx-3.25$.如果某天进店人数是75人,预测这一天该商品销售的件数为( )
| x | 10 | 15 | 20 | 25 | 30 | 35 | 40 |
| y | 5 | 6 | 12 | 14 | 20 | 23 | 25 |
| A. | 47 | B. | 52 | C. | 55 | D. | 38 |
16.已知直线方程为(2+m)x+(1-2m)y+4-3m=0.这条直线恒过一定点,这个定点坐标为( )
| A. | (-2m,-m-4) | B. | (5,1) | C. | (-1,-2) | D. | (2m,m+4) |