题目内容
17.三棱锥P-ABC中各条棱长都相等,点E是BC中点,则直线PE与AB所成角的余弦值为√36.分析 如图所示,取AC的中点F,连接EF,PF.则EF=∥12AB,可得∠PEF是异面直线PE与AB所成角或其补角.利用余弦定理即可得出.
解答 解:如图所示,取AC的中点F,连接EF,PF.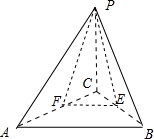
则EF=∥12AB,∴∠PEF是异面直线PE与AB所成角或其补角.
不妨设AB=2,则EF=1.
PE=PF=√3,
∴cos∠PEF=(√3)2+12−(√3)22×√3×1=√36.
∴直线PE与AB所成角的余弦值为√36.
故答案为:√36.
点评 本题考查了正四面体的性质、三角形中位线定理、余弦定理、异面直线所成的角,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.某商店对每天进店人数x与某种商品成交量y(单位:件)进行了统计,得到如下对应数据:
由表中数据,得线性回归方程为ˆy=ˆbx−3.25.如果某天进店人数是75人,预测这一天该商品销售的件数为( )
| x | 10 | 15 | 20 | 25 | 30 | 35 | 40 |
| y | 5 | 6 | 12 | 14 | 20 | 23 | 25 |
| A. | 47 | B. | 52 | C. | 55 | D. | 38 |
2.下列运算结果中,正确的是( )
| A. | a2a3=a5 | B. | (-a2)3=(-a3)2 | C. | (√a-1)0=1 | D. | (-a2)3=a6 |