题目内容
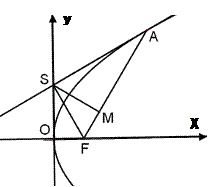
已知圆k过定点A(a,0)(a>0),圆心k在抛物线C: y2=2ax上运动,MN为圆k在y轴上截得的弦.
(1)试问MN的长是否随圆心k的运动而变化?
(2)当|OA|是|OM|与|ON|的等差中项时,抛物线C的准线与圆k有怎样的位置关系?
(1)试问MN的长是否随圆心k的运动而变化?
(2)当|OA|是|OM|与|ON|的等差中项时,抛物线C的准线与圆k有怎样的位置关系?
(1) 弦MN的长不随圆心k的运动而变化(2) 圆k必与准线相交
(1)设圆心k(x0,y0),且y02=2ax0,
圆k的半径R=|AK|=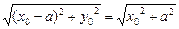
∴|MN|=2 =2a(定值)
=2a(定值)
∴弦MN的长不随圆心k的运动而变化.
(2)设M(0,y1)、N(0,y2)在圆k:(x-x0)2+(y-y0)2=x02+a2中,
令x=0,得y2-2y0y+y02-a2=0,∴y1y2=y02-a2
∵|OA|是|OM|与|ON|的等差中项.
∴|OM|+|ON|=|y1|+|y2|=2|OA|=2a.
又|MN|=|y1-y2|=2a,∴|y1|+|y2|=|y1-y2|
∴y1y2≤0,因此y02-a2≤0,即2ax0-a2≤0 ∴0≤x0≤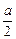 .
.
圆心k到抛物线准线距离d=x0+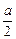 ≤a,而圆k半径R=
≤a,而圆k半径R= ≥a.
≥a.
且上两式不能同时取等号,故圆k必与准线相交.
圆k的半径R=|AK|=
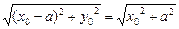
∴|MN|=2
 =2a(定值)
=2a(定值)∴弦MN的长不随圆心k的运动而变化.
(2)设M(0,y1)、N(0,y2)在圆k:(x-x0)2+(y-y0)2=x02+a2中,
令x=0,得y2-2y0y+y02-a2=0,∴y1y2=y02-a2
∵|OA|是|OM|与|ON|的等差中项.
∴|OM|+|ON|=|y1|+|y2|=2|OA|=2a.
又|MN|=|y1-y2|=2a,∴|y1|+|y2|=|y1-y2|
∴y1y2≤0,因此y02-a2≤0,即2ax0-a2≤0 ∴0≤x0≤
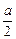 .
. 圆心k到抛物线准线距离d=x0+
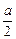 ≤a,而圆k半径R=
≤a,而圆k半径R= ≥a.
≥a. 且上两式不能同时取等号,故圆k必与准线相交.

练习册系列答案
相关题目
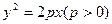 上一定点
上一定点
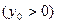 ,作直线分别交抛物线于
,作直线分别交抛物线于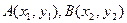
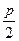 的点到焦点
的点到焦点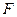 的距离;
的距离;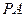 与
与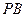 的斜率存在且倾斜角互补时,求
的斜率存在且倾斜角互补时,求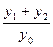 的值,并证明直线
的值,并证明直线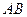 的斜率是非零常数。
的斜率是非零常数。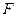 是抛物线
是抛物线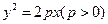 的焦点,过
的焦点,过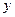 轴上的动点
轴上的动点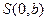 作直线
作直线 的垂线
的垂线 .
.
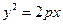 相切;
相切;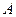 ,过点
,过点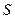 作直线
作直线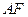 的垂线,垂足为
的垂线,垂足为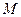 ,求线段
,求线段 的长度以及动点
的长度以及动点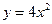 上求一点,使这点到直线
上求一点,使这点到直线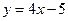 的距离最短。
的距离最短。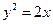 上,且与
上,且与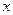 轴和该抛物线的准线都相切的一个圆的方程是( )
轴和该抛物线的准线都相切的一个圆的方程是( )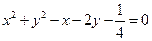
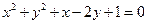

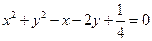
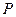 是抛物线
是抛物线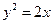 上的动点,焦点为
上的动点,焦点为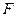 ,点
,点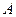 的坐标是
的坐标是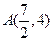 ,则
,则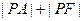 的最小值是( )
的最小值是( )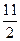
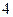
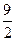
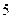
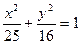 的中心为顶点,以椭圆的左准线为准线的抛物线与椭圆右准线交于A、B两点,则
的中心为顶点,以椭圆的左准线为准线的抛物线与椭圆右准线交于A、B两点,则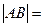 ________
________