题目内容
过抛物线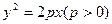 上一定点
上一定点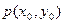
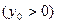 ,作直线分别交抛物线于
,作直线分别交抛物线于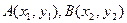
(1)求该抛物线上纵坐标为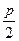 的点到焦点
的点到焦点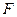 的距离;
的距离;
(2)当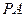 与
与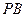 的斜率存在且倾斜角互补时,求
的斜率存在且倾斜角互补时,求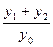 的值,并证明直线
的值,并证明直线 的斜率是非零常数。
的斜率是非零常数。
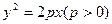 上一定点
上一定点
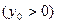 ,作直线分别交抛物线于
,作直线分别交抛物线于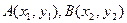
(1)求该抛物线上纵坐标为
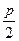 的点到焦点
的点到焦点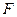 的距离;
的距离;(2)当
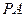 与
与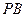 的斜率存在且倾斜角互补时,求
的斜率存在且倾斜角互补时,求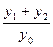 的值,并证明直线
的值,并证明直线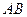 的斜率是非零常数。
的斜率是非零常数。(1)当 时,
时, ,又抛物线的准线方程为
,又抛物线的准线方程为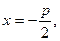
由抛物线的定义得,所求距离为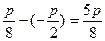
(2)设直线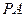 的斜率为
的斜率为 ,
,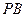 的斜率为
的斜率为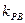 ,
,
由 ,
, ,得
,得 ,同理
,同理
由于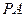 与
与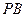 的斜率存在且倾斜角互补,因此
的斜率存在且倾斜角互补,因此
 即
即
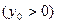 ,那么
,那么
再设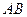 的斜率为
的斜率为 ,同上即得
,同上即得 ,将
,将 得
得 ,显然,是非零常数。
,显然,是非零常数。
 时,
时, ,又抛物线的准线方程为
,又抛物线的准线方程为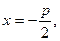
由抛物线的定义得,所求距离为
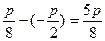
(2)设直线
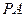 的斜率为
的斜率为 ,
,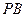 的斜率为
的斜率为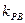 ,
,由
 ,
, ,得
,得 ,同理
,同理
由于
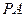 与
与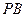 的斜率存在且倾斜角互补,因此
的斜率存在且倾斜角互补,因此
 即
即
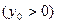 ,那么
,那么
再设
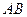 的斜率为
的斜率为 ,同上即得
,同上即得 ,将
,将 得
得 ,显然,是非零常数。
,显然,是非零常数。
练习册系列答案
相关题目
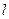

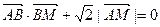 ,求动点M的轨迹C 的方程;
,求动点M的轨迹C 的方程;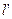 (斜率不等于零)与(1)中的轨迹C交于不同的两点E、F(E在B、F之间),且
(斜率不等于零)与(1)中的轨迹C交于不同的两点E、F(E在B、F之间),且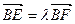 ,试求λ的取值范围。
,试求λ的取值范围。
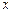 轴,抛物线上一点
轴,抛物线上一点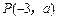 到焦点的距离为5,求抛物线的标准方程.
到焦点的距离为5,求抛物线的标准方程.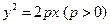 ,其焦点为F,一条过焦点F,倾斜角为
,其焦点为F,一条过焦点F,倾斜角为
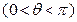 的直线交抛物线于A,B两点,连接AO(O为坐标原点),交准线于点
的直线交抛物线于A,B两点,连接AO(O为坐标原点),交准线于点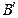 ,连接BO,交准线于点
,连接BO,交准线于点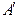 ,求四边形
,求四边形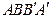 的面积.
的面积.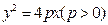 的准线与
的准线与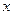 轴的交点为
轴的交点为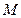 ,过点
,过点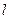 交抛物线于
交抛物线于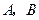 两点.若直线
两点.若直线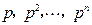 时,线段
时,线段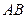 的垂直平分线与对称轴的交点依次为
的垂直平分线与对称轴的交点依次为 ,当
,当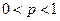 时,求
时,求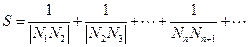 的值.
的值.