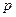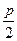题目内容
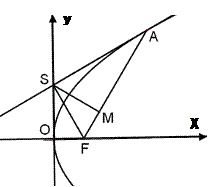
如图,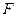 是抛物线
是抛物线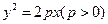 的焦点,过
的焦点,过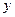 轴上的动点
轴上的动点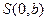 作直线
作直线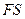 的垂线
的垂线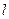 .
.
(Ⅰ)求证:直线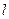 与抛物线
与抛物线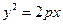 相切;
相切;
(Ⅱ)设直线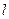 与抛物线
与抛物线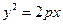 相切于点
相切于点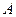 ,过点
,过点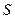 作直线
作直线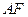 的垂线,垂足为
的垂线,垂足为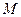 ,求线段
,求线段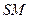 的长度以及动点
的长度以及动点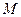 的轨迹方程.
的轨迹方程.
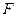 是抛物线
是抛物线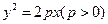 的焦点,过
的焦点,过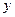 轴上的动点
轴上的动点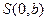 作直线
作直线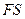 的垂线
的垂线 .
.
(Ⅰ)求证:直线
 与抛物线
与抛物线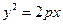 相切;
相切;(Ⅱ)设直线
 与抛物线
与抛物线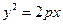 相切于点
相切于点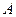 ,过点
,过点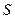 作直线
作直线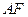 的垂线,垂足为
的垂线,垂足为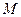 ,求线段
,求线段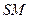 的长度以及动点
的长度以及动点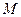 的轨迹方程.
的轨迹方程.(Ⅰ)证明略;
(Ⅱ) 动点
动点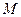 的轨迹是以点
的轨迹是以点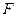 为圆心,
为圆心, 为半径的圆,其轨迹方程是
为半径的圆,其轨迹方程是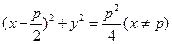
(Ⅱ)
 动点
动点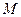 的轨迹是以点
的轨迹是以点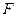 为圆心,
为圆心, 为半径的圆,其轨迹方程是
为半径的圆,其轨迹方程是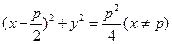
(Ⅰ)求证:抛物线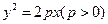 的焦点
的焦点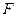 的坐标是(
的坐标是( ),
),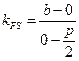 =
= ,∵
,∵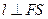 ,
,
∴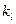 =
= ,∴直线
,∴直线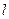 的方程是
的方程是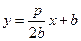 ,代入抛物线方程
,代入抛物线方程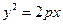 得
得
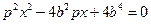 ,
,
其判别式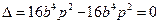 ,所以,直线
,所以,直线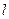 与抛物线
与抛物线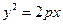 相切.
相切.
(Ⅱ)解:直线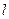 与抛物线
与抛物线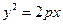 相切于点
相切于点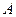 ,由
,由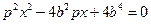 解得
解得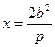 ,代入
,代入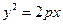 得
得 ,依图示可得点
,依图示可得点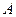 的坐标是(
的坐标是( ,
, ).所以
).所以
 ,
,
直线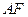 的方程是
的方程是 ,
,
点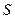 到直线
到直线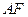 的距离
的距离 .
.
∵ ,
, ,
,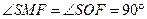 ,∴
,∴ ,
,
∴ ,∴动点
,∴动点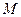 的轨迹是以点
的轨迹是以点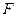 为圆心,
为圆心, 为半径的圆,其轨迹方程是
为半径的圆,其轨迹方程是
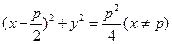 .
.
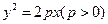 的焦点
的焦点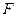 的坐标是(
的坐标是( ),
),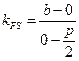 =
= ,∵
,∵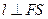 ,
,∴
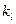 =
= ,∴直线
,∴直线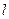 的方程是
的方程是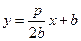 ,代入抛物线方程
,代入抛物线方程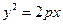 得
得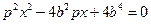 ,
,其判别式
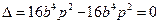 ,所以,直线
,所以,直线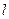 与抛物线
与抛物线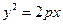 相切.
相切.(Ⅱ)解:直线
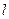 与抛物线
与抛物线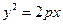 相切于点
相切于点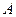 ,由
,由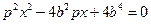 解得
解得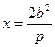 ,代入
,代入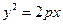 得
得 ,依图示可得点
,依图示可得点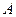 的坐标是(
的坐标是( ,
, ).所以
).所以 ,
,直线
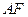 的方程是
的方程是 ,
, 点
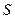 到直线
到直线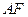 的距离
的距离 .
. ∵
 ,
, ,
,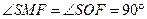 ,∴
,∴ ,
,∴
 ,∴动点
,∴动点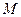 的轨迹是以点
的轨迹是以点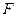 为圆心,
为圆心, 为半径的圆,其轨迹方程是
为半径的圆,其轨迹方程是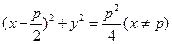 .
. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
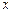 轴,抛物线上一点
轴,抛物线上一点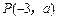 到焦点的距离为5,求抛物线的标准方程.
到焦点的距离为5,求抛物线的标准方程. ,焦点为
,焦点为 ,
, 是抛物线上的动点,则
是抛物线上的动点,则 的最大值为 .
的最大值为 .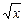 上,其横坐标依次为1,m,4(1<m<4),当△ABC的面积最大时,m等于( )
上,其横坐标依次为1,m,4(1<m<4),当△ABC的面积最大时,m等于( )


 所得的弦长为
所得的弦长为 。
。 的过焦点的弦为
的过焦点的弦为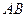 ,且
,且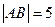 ,又
,又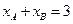 ,则
,则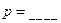
 过抛物线
过抛物线 的焦点,并且与
的焦点,并且与 轴垂直,若
轴垂直,若 ( )
( )

 的焦点
的焦点 的直线交抛物线于
的直线交抛物线于 两点,则
两点,则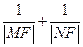 为定值,这个定值是( )
为定值,这个定值是( )