题目内容
10.设a1=1,an+1+$\sqrt{1-{a}_{n}}$=0,证明:$\underset{lim{a}_{n}}{n→∞}$存在,并求其极限.分析 当n→∞时,an+1=an,从而得${{a}_{n}}^{2}+{{a}_{n}-1=0}^{\;}$,由此能求出$\underset{lim{a}_{n}}{n→∞}$.
解答 证明:∵$\underset{lim}{n→∞}$(an+1-an)=0,a1=1,an+1+$\sqrt{1-{a}_{n}}$=0,
∴${a}_{n}+\sqrt{1-{a}_{n}}=0$,且an≤0,
∴${{a}_{n}}^{2}+{{a}_{n}-1=0}^{\;}$,
解得${a}_{n}=-\frac{\sqrt{5}+1}{2}$,或${a}_{n}=\frac{\sqrt{5}-1}{2}$(舍),
∴$\underset{lim{a}_{n}}{n→∞}$存在,且$\underset{lim{a}_{n}}{n→∞}$=-$\frac{\sqrt{5}+1}{2}$.
点评 本题考查数列的极限值是否存在的证明,是中档题,解题时要注意二次函数的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知随机变量Z服从二项分布B(n,p),且EZ=12,DZ=8,则P和n的值分别为( )
| A. | $\frac{1}{3}$,36 | B. | $\frac{2}{3}$,18 | C. | $\frac{1}{6}$,72 | D. | $\frac{1}{2}$,24 |
18.已知函数f(x)=lg(x2-2ax+2),若对任意的x1,x2∈(-∞,1]且x1≠x2,均有[f(x1)-f(x2)]( x1-x2 )<0成立,则实数a的取值范围是( )
| A. | (1,+∞) | B. | [1,+∞) | C. | (1,$\frac{3}{2}$) | D. | [1,$\frac{3}{2}$] |
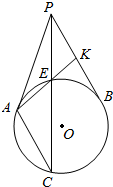 如图,点P为⊙O外一点,过点P作⊙O的两条切线,切点分别为A、B.过点A作PB的平行线,交⊙O于点C,连接PC,交⊙O于点E;连接AE,并延长AE交PB于点E,求证:PE•AC=CE•KB.
如图,点P为⊙O外一点,过点P作⊙O的两条切线,切点分别为A、B.过点A作PB的平行线,交⊙O于点C,连接PC,交⊙O于点E;连接AE,并延长AE交PB于点E,求证:PE•AC=CE•KB.