题目内容
20.已知随机变量Z服从二项分布B(n,p),且EZ=12,DZ=8,则P和n的值分别为( )| A. | $\frac{1}{3}$,36 | B. | $\frac{2}{3}$,18 | C. | $\frac{1}{6}$,72 | D. | $\frac{1}{2}$,24 |
分析 根据服从二项分布的随机变量其期望、方差公式可得关于n、p的方程组,解出即可.
解答 解:因为随机变量X服从二项分布B(n,p),
所以np=12①,np(1-p)=8②,
联立①②解得n=36,p=$\frac{1}{3}$,
故选:A.
点评 本题考查二项分布及随机变量的期望、方差,属基础题,熟记服从二项分布的随机变量的期望、方差公式是解决问题的关键.

练习册系列答案
相关题目
15.设A(-2,3),B(3,3),若直线ax+y+2=0与线段AB有交点,则实数a的取值范围是( )
| A. | [-$\frac{5}{3}$,$\frac{5}{2}$] | B. | (-∞,-$\frac{5}{3}$]∪[$\frac{5}{2}$,+∞) | C. | (-∞,-$\frac{5}{2}$]∪[$\frac{5}{3}$,+∞) | D. | [-$\frac{5}{2}$,$\frac{5}{3}$] |
12.函数y=log${\;}_{\frac{1}{2}}$(1-2x)的值域为( )
| A. | (-∞,+∞) | B. | (-∞,0) | C. | (0,+∞) | D. | (1,+∞) |
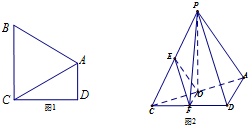 如图1,在直角梯形ABCD中,AD∥BC,∠ADC=90°,BA=BC=AC=2,把△BAC沿AC折起到△PAC的位置,使得P点在平面ADC上的正投影O恰好落在线段AC上,如图2所示.点E,F分别为棱PC,CD的中点.
如图1,在直角梯形ABCD中,AD∥BC,∠ADC=90°,BA=BC=AC=2,把△BAC沿AC折起到△PAC的位置,使得P点在平面ADC上的正投影O恰好落在线段AC上,如图2所示.点E,F分别为棱PC,CD的中点.