题目内容
【题目】为增强市民的节能环保意识，某市面向全市征召义务宣传志愿者．从符合条件的500名志愿者中随机抽取100名志愿者，其年龄频率分布直方图如图所示，其中年龄分组区间是：[20，25），[25，30），[30，35），[35，40），[40，45]．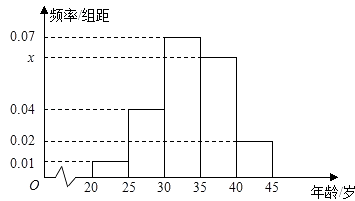
（Ⅰ）求图中x的值并根据频率分布直方图估计这500名志愿者中年龄在[35，40）岁的人数；
（Ⅱ）在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加中心广场的宣传活动，再从这20名中采用简单随机抽样方法选取3名志愿者担任主要负责人．记这3名志愿者中“年龄低于35岁”的人数为X，求X的分布列及数学期望．
【答案】解：（I）∵小矩形的面积等于频率，而频率之和等于1．
∴（0.07+x+0.04+0.02+0.01）×5=1，
解得x=0.06．
500名志愿者中，年龄在[35，40）岁的人数为0.06×5×500=150（人）．
（II）用分层抽样的方法，从100名志愿者中选取20名，
则其中年龄“低于35岁”的人有12名，
“年龄不低于35岁”的人有8名．
故X的可能取值为0，1，2，3，P（X=0）= 
= 
， 
= 
，
， 
= 
．
故X的分布列为
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
∴EX= 
= 
= 
【解析】（I）根据小矩形的面积等于频率，而频率之和等于1．即可得出x，再用频率×总体容量即可．（II）分层抽样的方法，从100名志愿者中选取20名；则其中年龄“低于35岁”的人有20×（0.01+0.04+0.07）×5=12名，“年龄不低于35岁”的人有8名．X的可能取值为0，1，2，3，再利用超几何分布即可得出，再利用数学期望的计算公式即可得出．
【考点精析】本题主要考查了离散型随机变量及其分布列的相关知识点，需要掌握在射击、产品检验等例子中，对于随机变量X可能取的值，我们可以按一定次序一一列出，这样的随机变量叫做离散型随机变量．离散型随机变量的分布列：一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn，X取每一个值 xi(i=1,2,......）的概率P(ξ=xi）＝Pi，则称表为离散型随机变量X 的概率分布，简称分布列才能正确解答此题．
