Question

【题目】记f（x）=|log2（ax）|在x∈[ ，8]时的最大值为g（a），则g（a）的最小值为（ ）
A.
B.2
C.
D.4

Answer 1

【答案】B
【解析】解：0＜a＜1的图象如图1
0＜a＜ 时：f（ ）=|log2（ a）|=log2 ，
f（2）=log2 ，f（ ）＞f（2），
即有g（a）=log2 ∈（2，+∞），
当 ≤a＜1时，f（ ）=|log2（ a）|
=log2 ，f（2）=log2（2a），f（ ）＞f（2），
即有g（a）=log2 ∈（1，2]；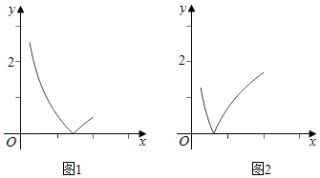

a≥1的图象如图2
当1≤a＜ 时，f（ ）=|log2（ a）|
=log2 ，f（2）=log2（2a），f（ ）＞f（2），
即有g（a）=log2 ∈（ ，1]；
当a≥ 时，f（ ）=|log2（ a）|
=log2 ，f（2）=log2（2a），f（ ）＜f（2），
即有g（a）=log2（2a）∈[ ，+∞）．
综上可得g（a）的范围是[ ，+∞）．
则M（a）的最小值为 ．
故选：B．
对a讨论，当0＜a＜ 时，当 ≤a＜1时，当1≤a＜ 时，当a≥ 时，通过图象，比较f（ ）和f（2）的大小，求得M（a）的范围，即可得到最小值