Question

【题目】已知函数

（1）若，证明；

（2）若，求的取值范围；并证明此时的极值存在且与无关.

Answer 1

【答案】（1）见解析（2）见解析

【解析】试题分析：

(1)利用题意求解导函数，求解 得到函数的单调递增区间，求解 得到函数的单调递减区间，由 可以得出结论；

(2)将 变形为，构造函数结合函数的性质即可求得实数 的取值范围；分类讨论 和两种情况即可证明此时的极值存在且与无关.

试题解析：

（1）若

当单调递减；当单调递增

所以，得证

（1）若，变形得到，

令，得到

，令，可得在单增，在单减，所以，

在单减，当所以，∴

（注：若令），得到

令，

，所以在单减，在单增，所以，

即在单增，当所以，∴

下面再证明的极值存在且与无关：

①,

与无关.

②

（其中）所以且在处取极小值

因为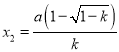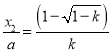，∴是关于的函数（与无关），

所以也是关于的函数（与无关）.