Question

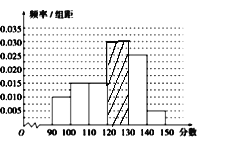
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生，按其数学成绩（均为整数）分成六组后得到如右部分频率分布直方图，观察图中的信息，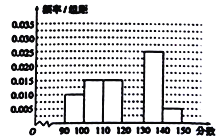

回答下列问题：

（1）补全频率分布直方图；并估计本次考试的数学平均成绩（同一组中的数据用该组区间的中点值作代表）；

（2）用分层抽样的方法在分数段为的学生成绩中抽取一个容量为6的样本，再从这6个样本中任取2人成绩，求至多有1人成绩在分数段内的概率.

Answer 1

【答案】（1）121（2）

【解析】试题分析：（1）根据频率分布直方图所有小长方形面积之和为1，求得分数在[120，130）内的频率，再除以组距得高，画出直方图；利用组中值与对应概率的积的和计算数学平均成绩（2）先根据分层抽样确定人数，利用枚举法确定所有基本事件数，从中确定至多有1人成绩在分数段内的事件数，最后根据古典概型概率公式计算概率

试题解析：分数在[120，130）内的频率（1）1-（0.1+0.15+0.15+0.25+0.05）=1-0.7=0.3，

因此补充的长方形的高为0.03。

估计平均分为

（2）由题意，[110，120）分数段的人数与[120，130）分数段的人数之比为1：2，

用分层抽样的方法在分数段为[110，130）的学生成绩中抽取一个容量为6的样本，

需在[110，120）分数段内抽取2人成绩，分别记为m，n；

在[120，130）分数段内抽取4人成绩，分别记为a，b，c，d；

设“从6个样本中任取2人成绩，至多有1人成绩在分数段[120，130）内”为事件A，

则基本事件共有{（m，n），（m，a），（m，b），（m，c），（m，d），（n，a），（n，b），（n，c），（n，d），（a，b），（a，c），（a，d），（b，c），（b，d）,（c，d）}，共15个．

事件A包含的基本事件有{（m，n），（m，a），（m，b），（m，c），（m，d），（n，a），（n，b），（n，c），（n，d）}共9个．

∴