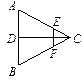题目内容
(本小题满分12分)
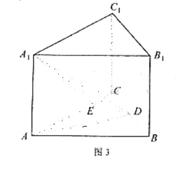
如图3,在正三棱柱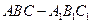 中,AB=4,
中,AB=4,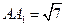 ,点D是BC的中点,
,点D是BC的中点,
点E在AC上,且DE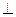
 E。
E。
(Ⅰ)证明:平面
 平面
平面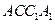 ;
;
(Ⅱ)求直线AD和平面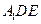 所成角的正弦值。
所成角的正弦值。
如图3,在正三棱柱
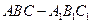 中,AB=4,
中,AB=4,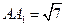 ,点D是BC的中点,
,点D是BC的中点,点E在AC上,且DE
 E。
E。
(Ⅰ)证明:平面
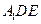
 平面
平面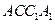 ;
;(Ⅱ)求直线AD和平面
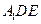 所成角的正弦值。
所成角的正弦值。(Ⅰ)证明见解析。
(Ⅱ)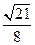
(Ⅱ)
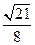
(Ⅰ)如图所示,由正三棱柱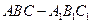 的性质知
的性质知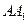
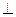 平面
平面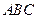 .
.
又DE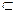 平面ABC,所以DE
平面ABC,所以DE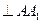 .而DE
.而DE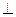
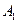 E,
E,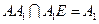 ,
,
所以DE⊥平面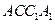 .又DE
.又DE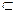 平面
平面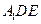 ,
,
故平面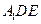 ⊥平面
⊥平面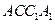 .
.
(Ⅱ)过点A作AF垂直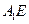 于点
于点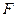 ,
,
连接DF.由(Ⅰ)知,平面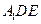 ⊥平面
⊥平面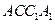 ,
,
所以AF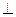 平面
平面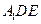 ,故
,故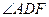 是直线AD和
是直线AD和
平面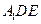 所成的角。因为DE
所成的角。因为DE
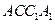 ,
,
所以DE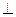 AC.而
AC.而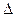 ABC是边长为4的正三角形,
ABC是边长为4的正三角形,
于是AD=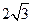 ,AE=4-CE=4-
,AE=4-CE=4-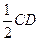 =3.
=3.
又因为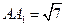 ,所以
,所以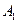 E=
E= 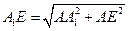
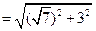 = 4,
= 4,
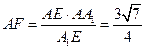 ,
, 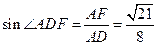 .
.
即直线AD和平面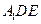 所成角的正弦值为
所成角的正弦值为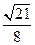 。
。
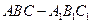 的性质知
的性质知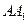
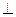 平面
平面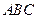 .
.又DE
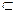 平面ABC,所以DE
平面ABC,所以DE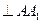 .而DE
.而DE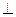
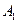 E,
E,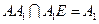 ,
,所以DE⊥平面
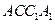 .又DE
.又DE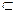 平面
平面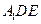 ,
,故平面
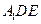 ⊥平面
⊥平面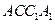 .
.(Ⅱ)过点A作AF垂直
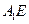 于点
于点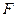 ,
,连接DF.由(Ⅰ)知,平面
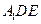 ⊥平面
⊥平面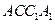 ,
,所以AF
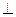 平面
平面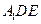 ,故
,故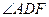 是直线AD和
是直线AD和平面
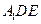 所成的角。因为DE
所成的角。因为DE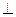
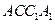 ,
,所以DE
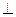 AC.而
AC.而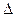 ABC是边长为4的正三角形,
ABC是边长为4的正三角形,于是AD=
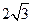 ,AE=4-CE=4-
,AE=4-CE=4-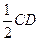 =3.
=3.又因为
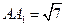 ,所以
,所以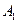 E=
E= 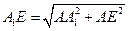
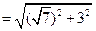 = 4,
= 4,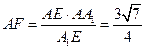 ,
, 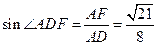 .
.即直线AD和平面
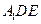 所成角的正弦值为
所成角的正弦值为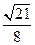 。
。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的底面为直角梯形,
的底面为直角梯形, ,
, ,
, ,
, ,
, 底面
底面 ,
, 为
为 的中点.
的中点. 平面
平面 ;
; 与平面
与平面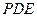 所成的角;
所成的角; 到平面
到平面
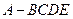 中,底面
中,底面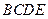 为矩形,侧面
为矩形,侧面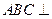 底面
底面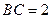 ,
,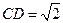 ,
,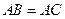 。
。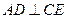 ;
;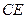 与平面
与平面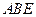 所成的角为
所成的角为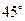 ,求二面角
,求二面角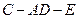 的大小。
的大小。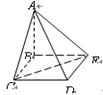
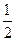 BD
BD
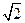 ,AC=3,BC=
,AC=3,BC=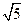 ,D是A1C的中点E是侧棱BB1上的一动点。
,D是A1C的中点E是侧棱BB1上的一动点。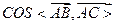 的值
的值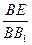 的值,不存在则说明理由。
的值,不存在则说明理由。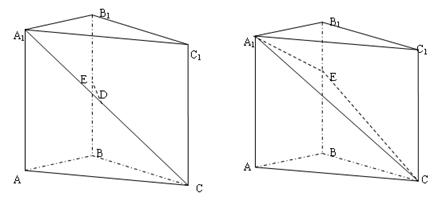
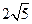 ,设这条最短路线与CC1的交
,设这条最短路线与CC1的交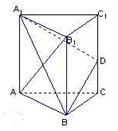
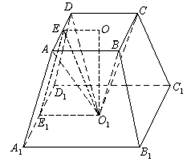
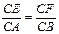 ,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).
,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).