题目内容
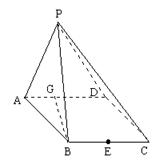
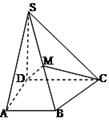
如图,已知三棱柱ABC-A1B1C1的所有棱长都相等,且侧棱垂直于底面,由
B沿棱柱侧面经过棱C C1到点A1的最短路线长为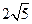 ,设这条最短路线与CC1的交
,设这条最短路线与CC1的交
点为D.
(1)求三棱柱ABC-A1B1C1的体积;
(2)在平面A1BD内是否存在过点D的直线与平面ABC平行?证明你的判断;
(3)证明:平面A1BD⊥平面A1ABB1.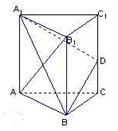
B沿棱柱侧面经过棱C C1到点A1的最短路线长为
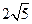 ,设这条最短路线与CC1的交
,设这条最短路线与CC1的交点为D.
(1)求三棱柱ABC-A1B1C1的体积;
(2)在平面A1BD内是否存在过点D的直线与平面ABC平行?证明你的判断;
(3)证明:平面A1BD⊥平面A1ABB1.

(1) (2)在平面A1BD内存在过点D的直线与平面ABC平行
(2)在平面A1BD内存在过点D的直线与平面ABC平行
(3)证明见解析
 (2)在平面A1BD内存在过点D的直线与平面ABC平行
(2)在平面A1BD内存在过点D的直线与平面ABC平行 (3)证明见解析
(1)如图,将侧面BB1C1C绕棱CC1旋转120°使其与侧面AA1C1C在同一平面上,点B运动到点B2的位置,连接A1B2,则A1B2就是由点B沿棱柱侧面经过棱CC1到点A1的最短路线。 ……………………………………1分
设棱柱的棱长为 ,则B2C=AC=AA1=
,则B2C=AC=AA1= ,
,
∵CD∥AA1 ∴D为CC1的中点,……………………………2分
在Rt△A1AB2中,由勾股定理得 ,
,
即 解得
解得 ,……………………4分
,……………………4分
∵ ∴
∴ ……………………………………6分
……………………………………6分
(2)设A1B与AB1的交点为O,连结BB2,OD,则 ……………………………7分
……………………………7分
∵ 平面
平面 ,
, 平面
平面 ∴
∴ 平面
平面 ,
,
即在平面A1BD内存在过点D的直线与平面ABC平行 ……………………………9分
(3)连结AD,B1D∵ ≌
≌ ≌
≌
∴ ∴
∴ ……………………………11分
……………………………11分
∵ ∴
∴ 平面A1ABB1 ……………………………13分
平面A1ABB1 ……………………………13分
又∵ 平面A1BD ∴平面A1BD⊥平面A1ABB1 ……………………………………14分
平面A1BD ∴平面A1BD⊥平面A1ABB1 ……………………………………14分
设棱柱的棱长为
 ,则B2C=AC=AA1=
,则B2C=AC=AA1= ,
,
∵CD∥AA1 ∴D为CC1的中点,……………………………2分
在Rt△A1AB2中,由勾股定理得
 ,
,即
 解得
解得 ,……………………4分
,……………………4分∵
 ∴
∴ ……………………………………6分
……………………………………6分(2)设A1B与AB1的交点为O,连结BB2,OD,则
 ……………………………7分
……………………………7分∵
 平面
平面 ,
, 平面
平面 ∴
∴ 平面
平面 ,
,即在平面A1BD内存在过点D的直线与平面ABC平行 ……………………………9分
(3)连结AD,B1D∵
 ≌
≌ ≌
≌
∴
 ∴
∴ ……………………………11分
……………………………11分∵
 ∴
∴ 平面A1ABB1 ……………………………13分
平面A1ABB1 ……………………………13分又∵
 平面A1BD ∴平面A1BD⊥平面A1ABB1 ……………………………………14分
平面A1BD ∴平面A1BD⊥平面A1ABB1 ……………………………………14分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
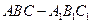 中,AB=4,
中,AB=4,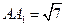 ,点D是BC的中点,
,点D是BC的中点,
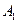 E。
E。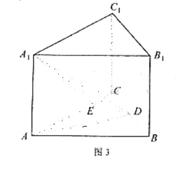
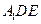
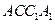 ;
;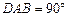 , AB∥CD,AD=CD=2AB=2,E,F分别是PC,CD的中点.
, AB∥CD,AD=CD=2AB=2,E,F分别是PC,CD的中点. ,
,
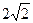 ,M为BC的中点
,M为BC的中点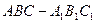 的底面边长是2,D是侧棱
的底面边长是2,D是侧棱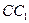 的中点,平面ABD和平面
的中点,平面ABD和平面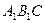 的交线为MN.
的交线为MN.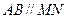 ;
;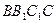 所成的角为
所成的角为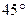 ,试求二面角
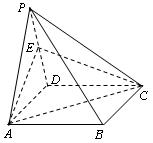
,试求二面角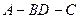 的大小.
的大小.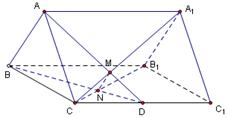
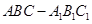 的侧面
的侧面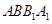 是圆柱的轴截面,
是圆柱的轴截面,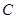 是圆柱底面圆周上不与
是圆柱底面圆周上不与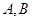 重合一个点。
重合一个点。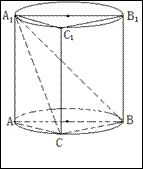
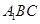
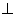 平面
平面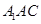 ;
;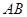 的中点时,求四棱锥
的中点时,求四棱锥 与圆柱的体积比。
与圆柱的体积比。 如图,PC⊥平面ABC,PM∥CB,∠ACB=120°,PM=AC=1,BC=2,异面直线AM与直线PC所成的角为60°.
如图,PC⊥平面ABC,PM∥CB,∠ACB=120°,PM=AC=1,BC=2,异面直线AM与直线PC所成的角为60°.