题目内容
【题目】已知函数![]() ,曲线y=f(x)在点(1,f(1))处的切线方程为y=x.
,曲线y=f(x)在点(1,f(1))处的切线方程为y=x.
(1)求函数f(x)的单调区间及极值;
(2)若x≥1,f(x)≤kx恒成立,求k的取值范围.
【答案】(1)单调增区间为![]() ,单调减区间为
,单调减区间为![]() ,
,![]() ,无极大值.(2)k≥1.
,无极大值.(2)k≥1.
【解析】
(1)可由切线方程求得a与b的值,再还原函数的导数,通过分类讨论得出函数的增减性
(2)可通过分离参数与构造函数的方法将参数问题转化为恒成立问题,利用导数进行求解
解:(1)f(x)的定义域为(0,+∞),![]() ,
,
故f′(1)=b-a=1,
又f(1)=a,点(1,a)在直线y=x上,
∴a=1,则b=2.
∴![]() 且,
且,![]() ,
,
当![]() 时,f′(x)<0,当
时,f′(x)<0,当![]() 时,f′(x)>0.
时,f′(x)>0.
故函数f(x)的单调增区间为![]() ,单调减区间为
,单调减区间为![]() ,
,
![]() ,无极大值.
,无极大值.
(2)由题意知,![]() 恒成立,
恒成立,
令![]() ,
,
则![]() ,
,
令h(x)=x-xlnx-1(x≥1),
则h′(x)=-lnx(x≥1),
当x≥1时,h′(x)≤0,h(x)在[1,+∞)上为减函数,
故h(x)≤h(1)=0,故g′(x)≤0,
∴g(x)在[1,+∞)上为减函数,
故g(x)的最大值为g(1)=1,∴k≥1.

【题目】某运动员射击一次所得环数![]() 的分布列如下:
的分布列如下:
| 8 | 9 | 10 |
| 0.4 | 0.4 | 0.2 |
现进行两次射击,且两次射击互不影响,以该运动员两次射击中最高环数作为他的成绩,记为![]() .
.
(1)求该运动员两次命中的环数相同的概率;
(2)求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
【题目】《基础教育课程改革纲要(试行)》将“具有良好的心理素质”列入新课程的培养目标.为加强心理健康教育工作的开展,不断提高学生的心理素质,九江市某校高二年级开设了《心理健康》选修课,学分为2分.学校根据学生平时上课表现给出“合格”与“不合格”两种评价,获得“合格”评价的学生给予50分的平时分,获得“不合格”评价的学生给予30分的平时分,另外还将进行一次测验.学生将以“平时分×40%+测验分×80%”作为“最终得分”,“最终得分”不少于60分者获得学分.
该校高二(1)班选修《心理健康》课的学生的平时份及测验分结果如下:
测验分 | [30,40) | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
平时分50分人数 | 0 | 3 | 4 | 4 | 2 | ||
平时分30分人数 | 1 | 0 | 0 |
(1)根据表中数据完成如下2×2列联表,并分析是否有95%的把握认为这些学生“测验分是否达到60分”与“平时分”有关联?
选修人数 | 测验分 达到60分 | 测验分 未达到60分 | 合计 |
平时分50分 | |||
平时分30分 | |||
合计 |
(2)若从这些学生中随机抽取1人,求该生获得学分的概率.
附: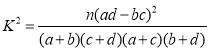 ,其中
,其中![]()
| 0.1 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |