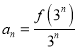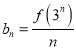题目内容
【题目】《基础教育课程改革纲要（试行）》将“具有良好的心理素质”列入新课程的培养目标.为加强心理健康教育工作的开展，不断提高学生的心理素质，九江市某校高二年级开设了《心理健康》选修课，学分为2分.学校根据学生平时上课表现给出“合格”与“不合格”两种评价，获得“合格”评价的学生给予50分的平时分，获得“不合格”评价的学生给予30分的平时分，另外还将进行一次测验.学生将以“平时分×40%+测验分×80%”作为“最终得分”，“最终得分”不少于60分者获得学分.
该校高二（1）班选修《心理健康》课的学生的平时份及测验分结果如下：
测验分 | [30，40） | [40，50） | [50，60） | [60，70） | [70，80） | [80，90） | [90，100] |
平时分50分人数 | 0 | 3 | 4 | 4 | 2 | ||
平时分30分人数 | 1 | 0 | 0 |
（1）根据表中数据完成如下2×2列联表，并分析是否有95%的把握认为这些学生“测验分是否达到60分”与“平时分”有关联?
选修人数 | 测验分 达到60分 | 测验分 未达到60分 | 合计 |
平时分50分 | |||
平时分30分 | |||
合计 |
（2）若从这些学生中随机抽取1人，求该生获得学分的概率.
附：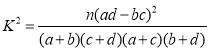
，其中
| 0.1 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【答案】（1）列联表见解析，有95%的把握认为学生“测验分是否达到60分”与“平时分”有关联（2）
【解析】
（1）先由题中数据完成表格,再计算
, 与
比较大小即可得到答案；
（2）根据表中数据,根据古典概型的概率公式求解.
（1）根据表中数据统计，可得2x2列联表
选修人数 | 测验分 | 合计 | |
达到60分 | 未达到60分 | ||
平时分50分 | 13 | 2 | 15 |
平时分30分 | 2 | 3 | 5 |
合计 | 15 | 5 | 20 |
，
，
∴有95%的把握认为学生“测验分是否达到60分”与“平时分”有关联；
（2）分析学生得分，
，
，平时分50分的学生中测验分只需达到50分，而平时分30分的学生中测验分必须达到60分，才能获得学分，
根据表中数据，平时分50分的学生测验分未达到50分的只有1人，平时分30分的学生测验分未达到60分的有3人，
∴从这些学生中随机抽取1人，该生获得学分的概率为
.
名校课堂系列答案
