��Ŀ����
13�������и����������У�������ȷ��������Ϊ�٢ڢۣ��ٺ���y=2x3+3x-1��ͼ����ڵ㣨0��1�������ĶԳƣ�
�ڶ�?x��y��R����x+y��0����x��1��y��-1��
����ʵ��x��y����x2+y2=1����$\frac{y}{x+2}$�����ֵΪ$\frac{{\sqrt{3}}}{3}$��
������ABC�����������sinA��cosB��
���ڡ�ABC�У�BC=5��G��O�ֱ�Ϊ��ABC�����ĺ����ģ���$\overrightarrow{OG}$•$\overrightarrow{BC}$=5�����ABC����״��ֱ�������Σ�
���� �ٸ��ݶԳ��ԵȺ����������ж�
���ɶ�ȫ�����ʵķ����ж�������٣�
�����ú������������ν�ϣ����Եõ���ȷ�Ľ��ۣ�
�ܽ�����Ǻ��������ʽ����жϼ���
���ڡ�ABC�У�G��O�ֱ�Ϊ��ABC�����ĺ����ģ�ȡBC���е�ΪD������AD��OD��GD���������ĺ����ĵ����ʣ����������������η�����е��������ʽ���Լ�������ƽ����Ϊģ��ƽ����
��� �⣺���ڢٺ���y=2x3-3x+1=��ͼ����ڵ㣨0��1�������ĶԳƣ�����㣨x0��y0���ں���ͼ���ϣ�������ڢٵ㣨0��1���ĶԳƵ�Ϊ��-x0��2-y0��Ҳ���㺯���Ľ���ʽ�������ȷ��
���ڢڶ�?x��y��R����x+y��0����Ӧ����ֱ��y=-x����ĵ㣬��x��1����y��-1������ȷ��
���ڢ���ʵ��x��y����x2+y2=1����$\frac{y}{x+2}$=$\frac{y-0}{x-��-2��}$�����Կ�����Բx2+y2=1�ϵĵ���㣨-2��0�����ߵ�б�ʣ������ֵΪ$\frac{\sqrt{3}}{3}$������ȷ��
���ڢ�����ABCΪ��������Σ���A��B����-A-B������ǣ�
����-A-B��$\frac{��}{2}$����A+B��$\frac{��}{2}$��B��$\frac{��}{2}$-A��
��cosB��cos��$\frac{��}{2}$-A����
��cosB��sinA���ʢܲ���ȷ��
���ڢ��ڡ�ABC�У�G��O�ֱ�Ϊ��ABC�����ĺ����ģ�
ȡBC���е�ΪD������AD��OD��GD����ͼ�� ��OD��BC��GD=$\frac{1}{3}$AD��
��OD��BC��GD=$\frac{1}{3}$AD��
��$\overrightarrow{OG}$=$\overrightarrow{OD}+\overrightarrow{DG}$|��$\overrightarrow{AD}=\frac{1}{2}��\overrightarrow{AB}+\overrightarrow{AC}��$
��$\overrightarrow{OG}•\overrightarrow{BC}=5$
��$��\overrightarrow{OD}+\overrightarrow{DG}��•\overrightarrow{BC}=\overrightarrow{DG}•\overrightarrow{BC}=-\frac{1}{6}$$��\overrightarrow{AB}+\overrightarrow{AC}��•\overrightarrow{BC}=5$��
��$-\frac{1}{6}•��\overrightarrow{AB}+\overrightarrow{AC}����\overrightarrow{AC}+\overrightarrow{AB}��=5$
��${\overrightarrow{AC}}^{2}-{\overrightarrow{AB}}^{2}=-30$
��BC=5
����$|\overrightarrow{AB}{|}^{2}=|\overrightarrow{AC}{|}^{2}+\frac{6}{5}|\overrightarrow{BC}{|}^{2}��|\overrightarrow{AC}{|}^{2}+|\overrightarrow{BC}{|}^{2}$
�����Ҷ����ɵ�cosC��0��
����CΪ�۽ǣ�
��������ABCΪ�۽������Σ��ݲ���ȷ��
�ʴ�Ϊ���٢ڢ�
���� ���⿼�������������������ʺ����á����Ǻ��������ʡ�������ٵ��жϵȣ�ʹ�������ν�ϵ�˼�룬����ѧ�еij���˼�룬Ҫ������ᣮ�ѶȽϴ�

| A�� | -3 | B�� | -2 | C�� | -1 | D�� | 2 |
| A�� | $\frac{1}{2}$ | B�� | $\frac{\sqrt{3}}{2}$ | C�� | $\frac{\sqrt{2}}{2}$ | D�� | $\frac{\sqrt{6}+\sqrt{2}}{4}$ |
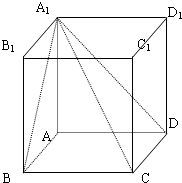 ��ͼ��������ABCD-A1B1C1D1��AA1=1������ABCD���ܳ�Ϊ4��
��ͼ��������ABCD-A1B1C1D1��AA1=1������ABCD���ܳ�Ϊ4��