题目内容
1.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点M(-2,-1),离心率为$\frac{\sqrt{2}}{2}$.过点M作倾斜角互补的两条直线分别与椭圆C交于异于M的另外两点P、Q.(Ⅰ)求椭圆C的方程;
(Ⅱ)证明:直线PQ的斜率为定值,并求这个定值;
(Ⅲ)∠PMQ能否为直角?证明你的结论.
分析 (Ⅰ)根据椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点M(-2,-1),离心率为$\frac{\sqrt{2}}{2}$,建立方程可求a,b的值,从而可得椭圆的方程;
(Ⅱ)设直线的倾斜角为α,β,则α+β=180°,α=β+∠PMQ,若∠PMQ=90°,则β=45°,α=135°,求出直线的方程与椭圆方程联立,验证即可得到结论;
(III)设直线MP的斜率为k,则直线MQ的斜率为-k,假设∠PMQ为直角,则k•(-k)=-1,k=±1,再验证即可求得结论.
解答 (Ⅰ)解:由题设,得$\frac{4}{{a}^{2}}+\frac{1}{{b}^{2}}$=1,①且$\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}$=$\frac{\sqrt{2}}{2}$,②
由①、②解得a2=6,b2=3,
椭圆C的方程为$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{3}=1$. …3分
(Ⅱ)证明:记P(x1,y1)、Q(x2,y2).由题意知,直线MP、MQ的斜率存在.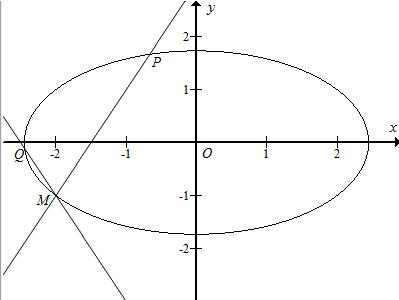
设直线MP的方程为y+1=k(x+2),与椭圆C的方程联立,得
(1+2k2)x2+(8k2-4k)x+8k2-8k-4=0,
-2,x1是该方程的两根,则-2x1=$\frac{8{k}^{2}-8k-4}{1+2{k}^{2}}$,x1=$\frac{-4{k}_{2}+4k+2}{1+2{k}^{2}}$.
设直线MQ的方程为y+1=-k(x+2),
同理得x2=$\frac{-4{k}_{2}-4k+2}{1+2{k}^{2}}$.…6分
因y1+1=k(x1+2),y2+1=-k(x2+2),
故kPQ=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{k({x}_{1}+{x}_{2}+4)}{{x}_{1}-{x}_{2}}$=1,
因此直线PQ的斜率为定值. …9分
(Ⅲ)解:设直线MP的斜率为k,则直线MQ的斜率为-k,
假设∠PMQ为直角,则k•(-k)=-1,k=±1.…11分
若k=1,则直线MQ方程y+1=-(x+2),
与椭圆C方程联立,得x2+4x+4=0,
该方程有两个相等的实数根-2,不合题意;
同理,若k=-1也不合题意.
故∠PMQ不可能为直角.…13分
点评 本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查直线斜率的计算,确定椭圆方程,联立方程是关键.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案| A. | -1,0,-1,0,… | B. | 1,11,111,1111,… | C. | 1,5,9,13,… | D. | 1,2,4,8,… |
| A. | $\left\{\begin{array}{l}{a=3}\\{b=-3}\end{array}\right.$或$\left\{\begin{array}{l}{a=-4}\\{b=11}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=-4}\\{b=11}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{a=-1}\\{b=5}\end{array}\right.$ | D. | 以上都不对 |
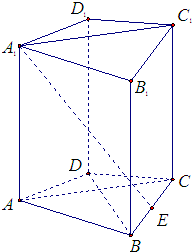 如图,在四棱柱ABCD-A1B1C1D1中,AB=BC=CA=$\sqrt{3}$,AD=CD=AA1=1,平面AA1C1C⊥平面ABCD,E为线段BC的中点,
如图,在四棱柱ABCD-A1B1C1D1中,AB=BC=CA=$\sqrt{3}$,AD=CD=AA1=1,平面AA1C1C⊥平面ABCD,E为线段BC的中点,