题目内容
5.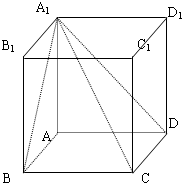 如图,长方体ABCD-A1B1C1D1的AA1=1,底面ABCD的周长为4.
如图,长方体ABCD-A1B1C1D1的AA1=1,底面ABCD的周长为4.(1)当长方体ABCD-A1B1C1D1的体积最大时,求二面角B-A1C-D的值;
(2)线段A1C上是否存在一点P,使得A1C⊥平面BPD,若有,求出P点的位置,没有请说明理由.
分析 (1)当长方体ABCD-A1B1C1D1的体积最大时,底面四边形ABCD为正方形,作BM⊥A1C于M,连接DM,BD,确定∠BMD即为所求二面角的平面角,△BMD中,根据余弦定理求二面角B-A1C-D的值;
(2)底面四边形ABCD为正方形,即只有ABCD为正方形时,线段A1C上存在点P满足要求,否则不存在.
解答 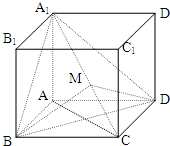 解:(1)根据题意,长方体体积为V=t(2-t)≤($\frac{t+2-t}{2}$)2=1 …2分
解:(1)根据题意,长方体体积为V=t(2-t)≤($\frac{t+2-t}{2}$)2=1 …2分
当且仅当t=2-t,即t=1时,体积V有最大值为1
所以当长方体ABCD-A1B1C1D1的体积最大时,底面四边形ABCD为正方形 …4分
作BM⊥A1C于M,连接DM,BD …5分
因为四边形ABCD为正方形,所以△A1BC与△A1DC全等,故DM⊥A1C,
所以∠BMD即为所求二面角的平面角 …6分
因为BC⊥平面AA1B1B,所以△A1BC为直角三角形
又A1B=$\sqrt{2}$,A1C=$\sqrt{3}$,所以BM=$\frac{\sqrt{6}}{3}$,同理可得,DM=$\frac{\sqrt{6}}{3}$.
在△BMD中,根据余弦定理有:cos∠BMD=$\frac{\frac{6}{9}+\frac{6}{9}-2}{2×\frac{\sqrt{6}}{3}×\frac{\sqrt{6}}{3}}$=-$\frac{1}{2}$ …8分
所以∠BMD=120°
即此时二面角B-A1C-D的值是120°.…9分
(2)若线段A1C上存在一点P,使得 A1C⊥平面BPD,则A1C⊥BD …10分
又A1A⊥平面ABCD,所以A1A⊥BD,所以BD⊥平面A1AC
所以BD⊥AC …12分
底面四边形ABCD为正方形,即只有ABCD为正方形时,线段A1C上存在点P满足要求,否则不存在
由(1)知,所求点P即为BM⊥A1C的垂足M
此时,A1P=$\frac{{A}_{1}{B}^{2}}{{A}_{1}C}$=$\frac{2\sqrt{3}}{3}$. …15分
点评 本题考查线面垂直,考查二面角的平面角,考查学生分析解决问题的能力,属于中档题.

| A. | $\frac{{\sqrt{3}}}{6}$ | B. | -$\frac{{\sqrt{3}}}{6}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | -$\frac{{\sqrt{3}}}{3}$ |
| A. | b2-4ac>0,a>0 | B. | b2-4ac>0 | C. | -$\frac{b}{2a}$>0 | D. | -$\frac{b}{2a}$<0 |
| A. | a<b<c | B. | c>b>a | C. | c<a<b | D. | c>a>b |
| A. | 2 | B. | 1 | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |