题目内容
18．
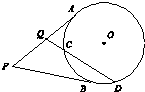如图，P为⊙O外一点，过P=点作⊙O的两条切线，切点分别为A，B，过PA的中点Q作割线交⊙O于C，D两点，若QC=1，CD=3，则PA=4．
分析 利用切割线定理可得QA2=QC•QD，可求QA，即可得PA．
解答 解：∵QA是⊙O的切线，
∴QA2=QC•QD，
∵QC=1，CD=3，
∴QA2=4，
∴QA=2，
∴PA=4，
故答案为：4．
点评 本题考查圆的切线长定理，考查切割线定理，考查学生的计算能力，属于基础题．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
已知椭圆C的中心在原点O，焦点在x轴上，离心率为$\frac{1}{2}$，右焦点到右顶点的距离为1
6．已知sinα+cos（π-α）=$\frac{1}{3}$，则sin2α的值为（ ）
| A． | $\frac{8}{9}$ | B． | $\frac{1}{9}$ | C． | $-\frac{8}{9}$ | D． | $\frac{4}{9}$ |
10．已知数列{an}满足2an+1+an=0，a2=1，则{an}的前9项和等于（ ）
| A． | -$\frac{2}{3}$（1-2-9） | B． | $\frac{1}{3}$（1-2-9） | C． | -$\frac{4}{3}$（1+2-9） | D． | （1-2-9） |
7．在某学校组织的一次利于定点投篮训练中，规定每人最多投3次；在A处每投进一球得3分，在B处每投进一球得2分；如果前两次得分之和超过3分即停止投篮，否则投第三次．某同学在A处的命中率q1为$\frac{1}{4}$，在B处的命中率为q2．该同学选择先在A处投一球，以后都在B处投，用ξ表示该同学投篮训练结束后所得的总分，其分布列为：
（I）求q2的值；
（Ⅱ）求随机变量ξ的数学期望．
| ξ | 0 | 2 | 3 | 4 | 5 |
| P | $\frac{3}{25}$ | p1 | p2 | p3 | p4 |
（Ⅱ）求随机变量ξ的数学期望．
如图，边长为2的正方形ABCD是圆柱的中截面，点E为线段BC的中点，点S为圆柱的下底面圆周上异于A，B的一个动点．