题目内容
7.在某学校组织的一次利于定点投篮训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投第三次.某同学在A处的命中率q1为$\frac{1}{4}$,在B处的命中率为q2.该同学选择先在A处投一球,以后都在B处投,用ξ表示该同学投篮训练结束后所得的总分,其分布列为:| ξ | 0 | 2 | 3 | 4 | 5 |
| P | $\frac{3}{25}$ | p1 | p2 | p3 | p4 |
(Ⅱ)求随机变量ξ的数学期望.
分析 (Ⅰ)由题设知,“ξ=0”对应的事件为“在三次投篮中没有一次投中”由对立事件和相互独立事件性质求的概率.
(Ⅱ)由题意列出随机变量的所有情况以及求出其概率继而得到期望.
解答 解:(Ⅰ)由题设知,“ξ=0”对应的事件为“在三次投篮中没有一次投中”
由对立事件和相互独立事件性质可知,
P(ξ=0)=(1-q1)$(1-{q}_{2})^{2}=\frac{3}{25}$
即$\frac{3}{4}(1-{q}_{2})^{2}=\frac{3}{25}$,解得${q}_{2}=\frac{3}{5}$
(Ⅱ)由题意知:
P1=P(ξ=2)=$(1-\frac{1}{4}){C}_{2}^{1}×\frac{3}{5}×\frac{2}{5}=\frac{36}{100}$,
P2=P(ξ=3)=$\frac{1}{4}×\frac{2}{5}×\frac{2}{5}=\frac{4}{100}$
P3=P(ξ=4)=$\frac{3}{4}×\frac{3}{5}×\frac{3}{5}=\frac{27}{100}$
P4=P(ξ=5)=$\frac{1}{4}×\frac{3}{5}+\frac{1}{4}×\frac{2}{5}×\frac{3}{5}=\frac{21}{100}$
∴Eξ=$0×\frac{3}{25}+2×\frac{36}{100}+3×\frac{4}{100}+4×\frac{27}{100}$$+5×\frac{21}{100}=\frac{288}{100}=2.88$
点评 本题主要考查了对立事件和相互独立事件爱你的性质以及随机变量的期望的求法,属中档题型.

练习册系列答案
相关题目
15.已知函数f(x)=ex+x2(x<0),g(x)=x2-4x+$\frac{9}{2}$+ln(x+t-2),若f(x)的图象上存在一点P,它关于直线x=1的对称点P′落在y=g(x)的图象上,则t的取值范围是( )
| A. | (-∞,$\frac{1}{\sqrt{e}}$) | B. | (-$\sqrt{e}$,$\frac{1}{\sqrt{e}}$) | C. | (-$\frac{1}{\sqrt{e}}$,$\sqrt{e}$) | D. | (0,$\sqrt{e}$) |
16.已知O为坐标原点,双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a,b>0)的右焦点F,以F为圆心,OF为半径作圆交双曲线的渐近线于异于原点的两点A、B,若$(\overrightarrow{AO}+\overrightarrow{AF})•\overrightarrow{OF}$<0,则双曲线的离心率e的取值范围为( )
| A. | $(1,\sqrt{2})$ | B. | (1,2) | C. | (2,+∞) | D. | $({1,\frac{1}{2}})$ |
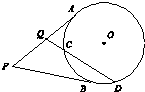 如图,P为⊙O外一点,过P=点作⊙O的两条切线,切点分别为A,B,过PA的中点Q作割线交⊙O于C,D两点,若QC=1,CD=3,则PA=4.
如图,P为⊙O外一点,过P=点作⊙O的两条切线,切点分别为A,B,过PA的中点Q作割线交⊙O于C,D两点,若QC=1,CD=3,则PA=4.