题目内容
8. 如图,边长为2的正方形ABCD是圆柱的中截面,点E为线段BC的中点,点S为圆柱的下底面圆周上异于A,B的一个动点.
如图,边长为2的正方形ABCD是圆柱的中截面,点E为线段BC的中点,点S为圆柱的下底面圆周上异于A,B的一个动点.(1)在圆柱的下底面上确定一定点F,使得EF∥平面ASC;
(2)求证:平面ASC⊥平面BSC.
分析 (1)证明EF∥AC,利用直线与平面平行的判定定理证明EF∥平面ASC.
(2)证明BC⊥AS,BS⊥AS,推出AS⊥平面BSC,…,然后证明平面ASC⊥平面BSC.
解答 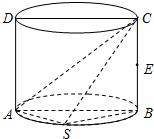 证明:(1)点F为线段AB的中点,又点E为线段BC的中点,
证明:(1)点F为线段AB的中点,又点E为线段BC的中点,
故EF∥AC,…(2分)
又AC?平面ASC,EF?平面ASC,
所以EF∥平面ASC.…(6分)
(2)因为正方形ABCD是圆柱的中截面,所以BC⊥底面ASB,
而AS?底面ASB,故BC⊥AS,…(8分)
因为点S为圆柱的下底面圆周上异于A,B的一个动点,所以BS⊥AS,…(10分)
又BC∪BS=B,且BC,BS?平面BSC,所以AS⊥平面BSC,…(12分)
又AS?平面ASC,所以,平面ASC⊥平面BSC.…(14分)
点评 本题考查直线与平面平行的判定定理,平面与平面垂直的判定定理的应用,考查空间想象能力以及逻辑推理能力.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
16.已知O为坐标原点,双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a,b>0)的右焦点F,以F为圆心,OF为半径作圆交双曲线的渐近线于异于原点的两点A、B,若$(\overrightarrow{AO}+\overrightarrow{AF})•\overrightarrow{OF}$<0,则双曲线的离心率e的取值范围为( )
| A. | $(1,\sqrt{2})$ | B. | (1,2) | C. | (2,+∞) | D. | $({1,\frac{1}{2}})$ |
3.设集合A=$\{x|-\frac{1}{2}<x<2\},B=\{x\left|{{x^2}≤1}\right.\}$,则A∪B=( )
| A. | $\{x|-\frac{1}{2}<x≤1\}$ | B. | {x|-1≤x<2} | C. | {x|x<2} | D. | {x|1≤x<2} |
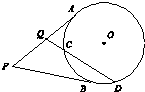 如图,P为⊙O外一点,过P=点作⊙O的两条切线,切点分别为A,B,过PA的中点Q作割线交⊙O于C,D两点,若QC=1,CD=3,则PA=4.
如图,P为⊙O外一点,过P=点作⊙O的两条切线,切点分别为A,B,过PA的中点Q作割线交⊙O于C,D两点,若QC=1,CD=3,则PA=4.