题目内容
6.已知sinα+cos(π-α)=$\frac{1}{3}$,则sin2α的值为( )| A. | $\frac{8}{9}$ | B. | $\frac{1}{9}$ | C. | $-\frac{8}{9}$ | D. | $\frac{4}{9}$ |
分析 由诱导公式和二倍角的正弦函数公式即可求值.
解答 解:∵sinα+cos(π-α)=$\frac{1}{3}$,
∴sinα-cosα=$\frac{1}{3}$,两边平方可得:1-sin2α=$\frac{1}{9}$,
∴sin2α=$\frac{8}{9}$.
故选:A.
点评 本题主要考查了诱导公式和二倍角的正弦函数公式的应用,属于基本知识的考查.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
15.已知函数f(x)=ex+x2(x<0),g(x)=x2-4x+$\frac{9}{2}$+ln(x+t-2),若f(x)的图象上存在一点P,它关于直线x=1的对称点P′落在y=g(x)的图象上,则t的取值范围是( )
| A. | (-∞,$\frac{1}{\sqrt{e}}$) | B. | (-$\sqrt{e}$,$\frac{1}{\sqrt{e}}$) | C. | (-$\frac{1}{\sqrt{e}}$,$\sqrt{e}$) | D. | (0,$\sqrt{e}$) |
16.已知O为坐标原点,双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a,b>0)的右焦点F,以F为圆心,OF为半径作圆交双曲线的渐近线于异于原点的两点A、B,若$(\overrightarrow{AO}+\overrightarrow{AF})•\overrightarrow{OF}$<0,则双曲线的离心率e的取值范围为( )
| A. | $(1,\sqrt{2})$ | B. | (1,2) | C. | (2,+∞) | D. | $({1,\frac{1}{2}})$ |
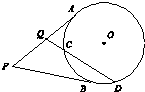 如图,P为⊙O外一点,过P=点作⊙O的两条切线,切点分别为A,B,过PA的中点Q作割线交⊙O于C,D两点,若QC=1,CD=3,则PA=4.
如图,P为⊙O外一点,过P=点作⊙O的两条切线,切点分别为A,B,过PA的中点Q作割线交⊙O于C,D两点,若QC=1,CD=3,则PA=4.