题目内容
8. 已知椭圆C的中心在原点O,焦点在x轴上,离心率为$\frac{1}{2}$,右焦点到右顶点的距离为1
已知椭圆C的中心在原点O,焦点在x轴上,离心率为$\frac{1}{2}$,右焦点到右顶点的距离为1(1)求椭圆C的方程;
(2)如图,动直线l:y=kx+m与椭圆C有且仅有一个公共点,点M、N是直线l上的两点F1、F2是椭圆的左右焦点,且F1M⊥l,F2N⊥l,求四边形F1MNF2面积S的最大值.
分析 (1)设椭圆C的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0),半焦距为c.依题意$e=\frac{c}{a}=\frac{1}{2}$,由右焦点到右顶点的距离为1,得a-c=1.可求得椭圆方程
(2)(2)将直线l的方程y=kx+m代入椭圆y的方程$\frac{x^2}{4}+\frac{y^2}{3}=1$中,得(3+4k2)x2+8kmx+4m2-12=0.利用四边形面积可得结论
解答 解:(1)设椭圆C的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0),半焦距为c.
依题意$e=\frac{c}{a}=\frac{1}{2}$,由右焦点到右顶点的距离为1,得a-c=1.
解得c=1,a=2.
所以b2=a2-c2=3.
所以椭圆C的标准方程是$\frac{x^2}{4}+\frac{y^2}{3}=1$.…(4分)
(2)将直线l的方程y=kx+m代入椭圆y的方程$\frac{x^2}{4}+\frac{y^2}{3}=1$中,
得(3+4k2)x2+8kmx+4m2-12=0
由直线与椭圆仅有一个公共点知△=64k2m2-4(4k2+3)(4m2-12)=0,
化简得:m2=4k2+3.
设${d_1}=|{{F_1}M}|=\frac{{|{-k+m}|}}{{\sqrt{{k^2}+1}}}$,${d_2}=|{{F_2}M}|=\frac{{|{k+m}|}}{{\sqrt{{k^2}+1}}}$,
∵${d_1}^2+{d_2}^2={(\frac{{|{-k+m}|}}{{\sqrt{{k^2}+1}}})^2}+{(\frac{{|{k+m}|}}{{\sqrt{{k^2}+1}}})^2}=\frac{{2({m^2}+{k^2})}}{{{k^2}+1}}=\frac{{2(5{k^2}+3)}}{{{k^2}+1}}$,${d_1}{d_2}=\frac{{|{-k+m}|}}{{\sqrt{{k^2}+1}}}•\frac{{|{k+m}|}}{{\sqrt{{k^2}+1}}}=\frac{{|{{m^2}-{k^2}}|}}{{{k^2}+1}}=\frac{{3{k^2}+3}}{{{k^2}+1}}=3$.
∴$|{MN}|=\sqrt{{{|{{F_1}{F_2}}|}^2}-{{({d_1}-{d_2})}^2}}$=$\sqrt{4-({d_1}^2+{d_2}^2-2{d_1}{d_2})}=\frac{2}{{\sqrt{{k^2}+1}}}$.…(8分)
四边形F1MNF2的面积$S=\frac{1}{2}|{MN}|({d_1}+{d_2})$=$\frac{1}{{\sqrt{{k^2}+1}}}({d_1}+{d_2})$,${S^2}=\frac{1}{{{k^2}+1}}({d_1}^2+{d_2}^2+2{d_1}{d_2})=\frac{{16{k^2}+12}}{{{{({k^2}+1)}^2}}}$=$16-4{(\frac{1}{{{k^2}+1}}-2)^2}≤12$.
当且仅当k=0时,${S^2}=12,S=2\sqrt{3}$,故${S_{max}}=2\sqrt{3}$.
所以四边形F1MNF2的面积S的最大值为$2\sqrt{3}$.…(12分)
点评 本题主要考查直线与椭圆得综合问题,属难题,高考题常作为压轴题出现.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案 在四棱柱ABCD-A′B′C′D′中,底面ABCD为正方形,侧棱AA′⊥底面ABCD,AB=2,AA′=4.给出下面五个命题:
在四棱柱ABCD-A′B′C′D′中,底面ABCD为正方形,侧棱AA′⊥底面ABCD,AB=2,AA′=4.给出下面五个命题: 如图已知椭圆G:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1、F2,设A(0,b),若△AF1F2为正三角形且周长为6.
如图已知椭圆G:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1、F2,设A(0,b),若△AF1F2为正三角形且周长为6. 如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=2$\sqrt{3}$,则PC与平面PAD所成角的大小为45°.
如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=2$\sqrt{3}$,则PC与平面PAD所成角的大小为45°.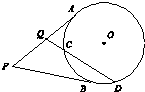 如图,P为⊙O外一点,过P=点作⊙O的两条切线,切点分别为A,B,过PA的中点Q作割线交⊙O于C,D两点,若QC=1,CD=3,则PA=4.
如图,P为⊙O外一点,过P=点作⊙O的两条切线,切点分别为A,B,过PA的中点Q作割线交⊙O于C,D两点,若QC=1,CD=3,则PA=4.