题目内容

9．7人排队，其中甲、乙、丙3人顺序一定，共有840不同的排法．

分析 根据题意，分2步进行分析：①先在7个位置中任取4个，安排除甲、乙、丙之外的3人，由排列数公式可得其情况数目，②在剩余3个位置安排3人，由于甲、乙、丙3人顺序一定，分析可得其情况数目；由分步计数原理计算可得答案．

解答 解：根据题意，假设有7个位置，对应7个人，
先在7个位置中任取4个，安排除甲、乙、丙之外的3人，有A74=840种情况，
由于甲、乙、丙3人顺序一定，在剩余3个位置安排3人即可，有1种情况，
则共有840×1=840种不同的排法；
故答案为：840．

点评 本题考查分步计数原理的应用，注意“甲、乙、丙3人顺序一定”这一条件，需要进行分类讨论．

练习册系列答案
相关题目
16．已知函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π），其图象经过点M（$\frac{π}{3}$，$\frac{1}{2}$），且与x轴两个相邻的交点的距离为π．
（1）求f（x）的解析式；
（2）在△ABC中，a=13，f（A）=$\frac{3}{5}$，f（B）=$\frac{5}{13}$，求△ABC的面积．
20．如图，四棱锥P-ABCD的底面ABCD是矩形，PA⊥平面ABCD，PA=AD=2，BD=2$\sqrt{3}$，则PC与平面PAD所成角的大小为45°．
17．已知数列{an}中，an+1=Sn-n+3，n∈N*，a1=2．
（1）求证：当n≥2时，n∈N*时，{an-1}是等比数列；
（2）求数列{an}的通项公式；
（3）设bn=$\frac{n}{{S}_{n}-n+2}$（n∈N*）的前n项和为Tn．求证：$\frac{1}{3}≤{T}_{n}＜\frac{4}{3}$（n∈N*）．
4．在等比数列{an}中，a6与a7的等差中项等于48，a4a5a6a7a8a9a10=1286，如果设{an}的前n项和为Sn，那么Sn=（　　）
A．5n-4B．4n-3C．3n-2D．2n-1
14．已知矩阵A=$[\begin{array}{l}{1}&{-2}\\{-2}&{-1}\end{array}]$，B=$[\begin{array}{l}{5}\\{-15}\end{array}]$满足AX=B，求矩阵X．
1．在△ABC中，内角A、B、C的对边分别为a、b、c，若其面积S=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{16}$，则cos2A=$\frac{255}{257}$．
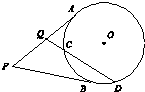18．如图，P为⊙O外一点，过P=点作⊙O的两条切线，切点分别为A，B，过PA的中点Q作割线交⊙O于C，D两点，若QC=1，CD=3，则PA=4．
19．已知f（x）=ex（x-a-1）-$\frac{1}{2}$x2+ax，a＞0．
（Ⅰ）讨论f（x）的单调性；
（Ⅱ）若x∈（0，1）时，f（x）＜-a-1，求a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网