题目内容
10.已知数列{an}满足2an+1+an=0,a2=1,则{an}的前9项和等于( )| A. | -$\frac{2}{3}$(1-2-9) | B. | $\frac{1}{3}$(1-2-9) | C. | -$\frac{4}{3}$(1+2-9) | D. | (1-2-9) |
分析 通过2an+1+an=0、a2=1可得数列{an}是以-2为首项、-$\frac{1}{2}$为公比的等比数列,计算即得结论.
解答 解:∵2an+1+an=0,a2=1,
∴a1=-2a2=-2,
又∵$\frac{{a}_{n+1}}{{a}_{n}}$=-$\frac{1}{2}$,∴数列{an}是以-2为首项、-$\frac{1}{2}$为公比的等比数列,
∴Sn=$\frac{-2[1-(-\frac{1}{2})^{n}]}{1-(-\frac{1}{2})}$=$\frac{4}{3}$[(-1)n•2-n-1],
∴S9=$\frac{4}{3}$(-2-9-1)=-$\frac{4}{3}$(1+2-9),
故选:C.
点评 本题考查求数列的和,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
15.已知函数f(x)=ex+x2(x<0),g(x)=x2-4x+$\frac{9}{2}$+ln(x+t-2),若f(x)的图象上存在一点P,它关于直线x=1的对称点P′落在y=g(x)的图象上,则t的取值范围是( )
| A. | (-∞,$\frac{1}{\sqrt{e}}$) | B. | (-$\sqrt{e}$,$\frac{1}{\sqrt{e}}$) | C. | (-$\frac{1}{\sqrt{e}}$,$\sqrt{e}$) | D. | (0,$\sqrt{e}$) |
 如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=2$\sqrt{3}$,则PC与平面PAD所成角的大小为45°.
如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=2$\sqrt{3}$,则PC与平面PAD所成角的大小为45°.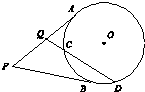 如图,P为⊙O外一点,过P=点作⊙O的两条切线,切点分别为A,B,过PA的中点Q作割线交⊙O于C,D两点,若QC=1,CD=3,则PA=4.
如图,P为⊙O外一点,过P=点作⊙O的两条切线,切点分别为A,B,过PA的中点Q作割线交⊙O于C,D两点,若QC=1,CD=3,则PA=4.